FourierSeries`

FourierCoefficient

As of Version 7.0, FourierCoefficient is part of the built-in Wolfram Language kernel.

FourierCoefficient[expr,t,n]

gives the n coefficient in the Fourier exponential series expansion of expr, where expr is a periodic function of t with period 1.

Details and Options

To use FourierCoefficient, you first need to load the Fourier Series Package using Needs["FourierSeries`"].
The n 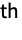coefficient in the Fourier exponential series expansion of expr is by default defined to be Integrate[expr ^2πnt,{t,-,}].
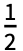If n is numeric, it should be an explicit integer.
Different choices for the definition of the Fourier exponential series expansion can be specified using the option FourierParameters.
With the setting FourierParameters->{a,b}, expr is assumed to have a period of , and the n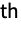 coefficient computed by FourierCoefficient is Integrate[expr ^{2 πbnt},{t,-,}].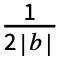
In addition to the option FourierParameters, FourierCoefficient can also accept the options available to Integrate. These options are passed directly to Integrate.