NDSolve`FEM`

EvaluateOnElementMesh

EvaluateOnElementMesh[{x₁,…},f,mesh]

returns an InterpolatingFunction where f depending on formal parameters {x₁,…} was evaluated on the ElementMesh mesh.

EvaluateOnElementMesh[{x₁,…},{f₁,…},mesh]

evaluates multiple expressions {f₁,…} on the same mesh mesh.

EvaluateOnElementMesh[{x₁,…},f,mesh]

returns a DiscontinuousInterpolatingFunction if mesh has multiple material regions.

Details and Options

EvaluateOnElementMesh either returns an InterpolatingFunction or a DiscontinuousInterpolatingFunction.
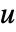The interpolating function is created by solving a system of equations where the solution is the values at the nodes of the mesh. 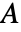is the discretized matrix of the weak form of 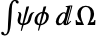, with shape function and test function .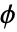
EvaluateOnElementMesh never evaluates at mesh nodes, but evaluates at the integration point of the mesh elements.
EvaluateOnElementMesh has the following options:

"DiscontinuousInterpolation"	Automatic	switch off automatic discontinuity handling
"ExtrapolationHandler"	Automatic	specify how extrapolation is handled
"MarkerPriority"	Automatic	speficy behavior at the boundary

Examples

open allclose all

Basic Examples (2)

Load the package:

Generate an element mesh for a disk:

Evaluate the function on the mesh:

Visualize the solution:

Create and visualize a multi-material ElementMesh:

Create a function that is discontinuous in the material region:

Evaluate the discontinuous function on the mesh:

Visualize the discontinuous interpolation function:

Options (3)

"DiscontinuousInterpolation" (1)

Discontinuous interpolation is the default, if a mesh with several material markers is given. In case discontinuous interpolation is not wanted, it can be turned off with the option "DiscontinuousInterpolation"  False.

Generate and visualize a mesh with multiple regions:

Create a function that is discontinuous in the material region:

Evaluate the discontinuous function on the mesh:

Evaluate the discontinuous function on the mesh but generate an InterpolatingFunction:

"ExtrapolationHandler" (1)

By default, the InterpolatingFunction or the DiscontinuousInterpolatingFunction generated through EvaluateOnElementMesh will handle extrapolation by giving a warning message and performing an extrapolation. This behavior can be changed.

Evaluate the function on the mesh:

Query the InterpolatingFunction outside of its domain:

Construct an InterpolatingFunction with an extrapolation handler that returns Indeterminate for queries outside the domain:

Construct an InterpolatingFunction with an extrapolation handler that extrapolates and does not give a warning message for queries outside the domain:

More information on extrapolation handling can be found in ElementMeshInterpolation.

"MarkerPriority" (1)

Specifying a marker priority allows you to control which value will be used at the material interface. Consider this 1D example mesh:

The mesh has markers 10 and 20:

Write a function that will give a value of –1 for all elements with marker 10 and a value of 1 for all other elements:

Create a discontinuous interpolating function:

Visualize the function:

Evaluate the discontinuous function at the interface position at :

By inspecting the marker priority of the discontinuous interpolating function, you can see that the marker 10 precedes the marker 20. This means values associated with marker 10 will have a higher precedence than the values associated with marker 10:

The value at the interface can be set by changing the precedence of the markers:

Now, the marker priority has changed:

The value at the interface position has changed to the value associated with marker 20:

The overall plot looks the same, as only the value at the interface has changed:

Possible Issues (1)

Computing a gradient of an InterpolatingFunction with EvaluateOnElementMesh can be problematic.

Create a multi-material mesh:

Set up the partial differential equation with a discontinuous coefficient:

Set up boundary conditions:

Solve the equation:

Visualize the solution:

Find the gradient of the solution on the mesh:

Visualize the gradient in the direction along the axis:

A continuous value would be expected. The comes up because the gradient was computed on the interpolating function directly and then that was evaluated on the element mesh. A better approach is to first convert the interpolating function to a DiscontinuousInterpolatingFunction:

Compute the gradient on of the DiscontinuousInterpolatingFunction:

Visualize the gradient in the direction along the axis at :