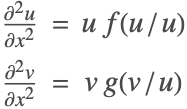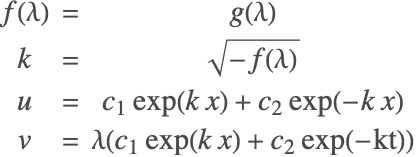Nonlinear Finite Element Method Verification Tests

Stationary TestsTest Result Inspection
Transient TestsReferences

This notebook contains tests that verify that the nonlinear Finite Element method works as expected. To run all tests, SelectAll and press Shift+Enter. The results will then be in the section Test Result Inspection.

Differential equations in tests are typically given in inactive form. In some cases, an inactive form of a differential equation is the only way to set a specific differential equation. The exact details of when an inactive equation is used are explained in the Finite Element Method Usage Tips tutorial. The sections about Formal Partial Differential Equations and NeumannValue and Formal Partial Differential Equations are particularly relevant. In the test suite, most tests would not strictly need an inactive form, but they are present so that the parsing of the equations can also be tested.

Note that these tests can also serve as a basis for developing your own differential equation models. As such, the tests are grouped into stationary (time-independent) and transient (time-dependent) tests. The next level of grouping is in the number of equations. Either a single equation or a coupled equation is considered. In those categories, one- and two-dimensional tests can be found. The fact that no three-dimensional tests are present is due to implementation of the finite element code. The code base for all dimensions is the same, and not much benefit would come from including three-dimensional tests.

Some cells in the actual tests are not evaluatable. These are mainly cells that contain a symbolic derivation and would take additional runtime and consume memory. If an actual analytical solution exists, it is given as a function. The derivation is there for inspection. To make these cells evaluatable, select the cells in question and choose Cell ▶ Cell Properties and make sure "Evaluatable" is ticked.

The individual subtest also needs to be evaluated in order to work as intended.

This loads the Finite Element package:
Set up options that force the use of the Finite Element Method.
To avoid keeping memory-intensive previous results, set the history length to 0.

Stationary Tests

This section contains examples of stationary (non-time-dependent) nonlinear partial differential equations.

1D Single Equation

This section contains examples of ordinary nonlinear differential equations with one equation. Ordinary differential equations with one independent variable are a special case of partial differential equations that usually deal with more than one independent variable.

Diffusion—FEM-NL-Stationary-1D-Single-Diffusion-0001

Test Reference:

[1], chapter 7, page 341.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution.
Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Test 1:
Test the inactive PDE.
Test 2:
Test the active PDE.
Test 3:
Test the low-level functions with step and evaluation count monitoring.

Diffusion—FEM-NL-Stationary-1D-Single-Diffusion-0002

Test Reference:

[4], page 38

Equation:

The right-hand-side f will be computed from the analytical solution.

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up the analytical solution.
Set up the right-hand-side f.
Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3:
Test the low-level functions with multiple mesh blocks.

Convection—FEM-NL-Stationary-1D-Single-Convection-0001

Test Reference:

[2], problems: 3.7, page 83.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution.
Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3:
Test the low-level functions and monitor steps and evaluations.

Convection—FEM-NL-Stationary-1D-Single-Convection-0002

Test Reference:

None

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution.
Check the analytical solution.
Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3:
Test the low-level functions and monitor steps and evaluations.

Reaction—FEM-NL-Stationary-1D-Single-Reaction-0001

Test Reference:

[1], problem 7.1, page 383.

Equation:

Set up the equation in inactive form.
Analytical solution:

None

Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Alternative numerical solution:
Set up an alternative numerical solution.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3:
Test the low-level functions and monitor steps and evaluations.

Reaction—FEM-NL-Stationary-1D-Single-Reaction-0002

Test Reference:

[1], problem 7.3, page 384.

Equation:

Set up the equation in inactive form.
Analytical solution:

None

Boundary conditions:

and

Set up the boundary conditions.
Region:

Set up the region.
Alternative numerical solution:
Set up an alternative numerical solution.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3 & 4:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.
Test an alternative formulation of low-level functions.

Reaction—FEM-NL-Stationary-1D-Single-Reaction-0003

Test Reference:

None

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Region:

The test uses an arbitrary region.

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3 & 4:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.
Test an alternative formulation of low-level functions.

Reaction—FEM-NL-Stationary-1D-Single-Reaction-0004

Test Reference:

None

Equation:

Set up the equation in inactive form.
Analytical solution:

-(-1)5/6

Set up the analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Region:

The test uses an arbitrary region.

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3 & 4:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.
Test an alternative formulation of low-level functions.

Load—FEM-NL-Stationary-1D-Single-Load-0001

Test Reference:

[3], Exact Solutions > Ordinary Differential Equations > Second-Order Nonlinear Ordinary Differential Equations; Equation 3.1.1; Autonomous equation.

Equation:

Set up the equation in inactive form.
Analytical solution:

where C1 and C2 are arbitrary constants.

Set up the analytical solution.
Check the analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Region:

The test uses an arbitrary region.

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3:
Test the low-level functions and monitor steps and evaluations.

Load—FEM-NL-Stationary-1D-Single-Load-0002

Test Reference:

[2], problem 3.17, page 84.

Equation:

Set up the equation in inactive form.
Analytical solution:

with

where λi are the roots of the equation

Set up the analytical solution.
Boundary conditions:

and

Set up the boundary conditions.
Region:

The test uses an arbitrary region.

Set up the region.
Test 1:
Test the inactive PDE with an initial seed to obtain one solution.
Test 2:
Test the inactive PDE with a different initial seed to obtain a different solution.
Test 3:
Test the PDE.
Test 4:
Test the active PDE with a different initial seed to obtain a different solution.

Radiation BC—FEM-NL-Stationary-1D-Single-Radiation-0001

Test Reference:

[1], problem 7.13, page 385.

The model problem is modified to allow for an analytical solution for comparison and extends the testing of the nonlinear boundary condition.

Equation:

Two changes are made to the parameters given in [1]. First, T∞ is given a nonzero value to extend the scope of the test, and second, P is set to 0 to allow for an analytical solution.

Specify the parameters.
Set up the equation in inactive form.
Analytical solution:

At position L, the solution of u can be found to be (derivation follows):

The solution at L.

What follows is the derivation of the solution at L. The cells are not evaluatable to not consume time when running the tests.

The structure of the general solution is as follows.
Note the following.
Specify a first constraint implied by the DirichletCondition at x=0.
Specify a second constraint implied from c2.
Use the definition of the generalized Neumann value and insert constraints.
Use Reduce the find the real, positive root.
Boundary conditions:

and

Set up the boundary conditions.
Region:

The test uses an arbitrary region.

Set up the region.
Test 1:
Test the inactive PDE with an initial seed to obtain one solution.
Test 2:
Test the active PDE with an initial seed to obtain one solution.
Test 3:
Test the low-level functions and monitor steps and evaluations.

1D Systems of Equations

This section contains examples of systems of ordinary nonlinear differential equations.

Reaction—FEM-NL-Stationary-1D-System-Reaction-0001

Test Reference:

[3], Exact Solutions > Systems of Ordinary Differential Equations > Nonlinear Systems of Two Ordinary Differential Equations, 3.2.7

Equation:

Set up the equation for specific values of f and g.
Analytical solution:

Set up the analytical solutions.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

Set up the boundary conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.
Test 3 & 4:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.
Test an alternative formulation of low-level functions.

2D Single Equation

This section contains examples of nonlinear partial differential equations with one equation.

Diffusion—FEM-NL-Stationary-2D-Single-Diffusion-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations > Other Second-Order Partial Differential Equations; Equation 4.1.2; Equation of steady transonic gas flow.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution with arbitrary constants C[1], C[2], C[3], C[4], a and b.
Verify the analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

Set up the boundary conditions.
Region:

Set up the region.
Tests 1:
Test the PDE in inactive form.
Tests 2:

In the activated case, the linearization leads to a higher-than-first-order derivative in the PDE coefficients, which can not be handled.

Test the PDE.
Test 3:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.

Reaction—FEM-NL-Stationary-2D-Single-Reaction-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations > Second-Order Elliptic Partial Differential Equations; Equation 3.1.2;

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up the analytical solution with arbitrary constants C[1] and C[1].
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

Set up the boundary conditions.
Region:

Set up the region.
Tests 1:
Test the PDE in inactive form.
Tests 2:
Test the PDE.
Tests 3 & 4:
Set up the low-level function data structures.
Test the low-level functions and monitor steps and evaluations.
Test an alternative formulation of low-level functions.

Transient Tests

This section contains examples of time-dependent nonlinear partial differential equations used for testing.

1D Single Equation

This section contains examples of time dependent ordinary nonlinear differential equations with one equation. Ordinary differential equations with one independent variable are a special case of partial differential equations that usually deal with more than one independent variable.

Diffusion—FEM-NL-Transient-1D-Single-Diffusion-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Heat Equation with a Power-Law Nonlinearity; Equation 1.2.1; Heat equation with a power-law nonlinearity.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Diffusion—FEM-NL-Transient-1D-Single-Diffusion-0002

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Heat Equation with a Exponential Nonlinearity; Equation 1.2.7; Heat Equation with a Exponential Nonlinearity.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Diffusion—FEM-NL-Transient-1D-Single-Diffusion-0003

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations > Second-Order Hyperbolic Partial Differential Equations; Equation 2.2.1;

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.

Convection—FEM-NL-Transient-1D-Single-Convection-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Burgers Equation; Equation 1.3.1; Burgers equation.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Convection—FEM-NL-Transient-1D-Single-Convection-0002

Test Reference:

https://mathematica.stackexchange.com/q/10453/18437

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

Boundary conditions are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

Initial conditions are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Reaction—FEM-NL-Transient-1D-Single-Reaction-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Fisher Equation; Equation 1.1.1; Fisher equation.

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Reaction—FEM-NL-Transient-1D-Single-Reaction-0002

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Hyperbolic Partial Differential Equations > Klein–Gordon Equation with a Power-Law Nonlinearity; Equation 2.1.1; Klein--Gordon equation with a power-law nonlinearity.

Equation:

Set up the equation in inactive form.
Analytical solution:

, ,

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Load—FEM-NL-Transient-1D-Single-Load-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Equation 1.1.5;

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the PDE.

Load—FEM-NL-Transient-1D-Single-Load-0002

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Hyperbolic Partial Differential Equations > Modified Liouville Equation; Equation 2.1.3;

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test 2:
Test the PDE.
Test 3:

Note that the activated test "FEM-NL-Transient-1D-Single-Load-0002-B" has a smaller norm than the inactive test "FEM-NL-Transient-1D-Single-Load-0002-A". This is because of the different formulation the time integration takes smaller time steps in the activated case. This is expected. You can change the behavior by either setting a "MaxStepSize" or by using a slightly different inactive formulation.

Lower the limit time step size.
Reformulate the inactive PDE.

Reaction-Diffusion—FEM-NL-Transient-1D-Single-Reaction-Diffusion-0001

Test Reference:

[3], Exact Solutions > Nonlinear Partial Differential Equations >Second-Order Parabolic Partial Differential Equations > Fisher Equation; Equation 1.2.5;

Equation:

Set up the equation in inactive form.
Analytical solution:

Set up solution parameters.
Set up an analytical solution.
Boundary conditions:

No boundary conditions are specified; they are deduced from the analytical solution.

and

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Test 1:
Test the PDE in inactive form.
Test 2:
Test the activated PDE.

2D Single Equation

This section contains examples of time-dependent partial nonlinear differential equations with one equation.

Diffusion—FEM-NL-Stationary-2D-Single-Diffusion-0001

Test Reference:

[5], Example 6.3.6, page 100

Equation:

Set up the equation in inactive form.
Analytical solution:

None

Manufactured solution

Set up the analytical solution.
Construct the right-hand side of the manufactured solution.
Boundary conditions:

Set up the boundary conditions.
Initial conditions:

No initial conditions are specified; they are deduced from the analytical solution.

Set up the initial conditions.
Region:

Set up the region.
Tests 1:
Test the PDE in inactive form.

A higher-quality result can be achieved by reducing the max cell measure of the mesh and further reducing the max step size. This is not done here because the test will run longer.

Test Result Inspection

This section contains the evaluation of the test runs. It works by collecting all instances of TestResultObject and generating a TestReport.

Extract TestResultObject from the notebook and generate a TestReport.
Inspect the failed tests run.

If the preceding table is empty, all tests succeeded.

References

[1] Advanced Topics in Finite Element Analysis of Structures; Bhatti, M. Asghar; Wiley; ISBN: 978-81-265-4537-7.

[2] Nonlinear Finite Element Analysis; Reddy, J. N.; Oxford; ISBN: 978-0-19-852529-5.

[3] "EqWorld, The World of Mathematical Equations"; http://eqworld.ipmnet.ru.

[4] Automated Solution of Differential Equations by the Finite Element Method; Logg, A; Mardal, K-A; Wells, G. N.; Springer; ISBN: 978-3-642-23098-1.

[5] "Nonlinear, Transient Conduction Heat Transfer Using a Discontinuous Galerkin Hierarchical Finite Element Method"; Sanders, J. C.; http://www.phys.uconn.edu/~sanders/ThesisMain.pdf.