仮説検定パッケージ
このパッケージには，データと 
値からの信頼区間，および正規分布に関連する分布の信頼区間を計算するための関数が含まれている．
分布の 
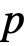値
正規分布，
分布，スチューデントの 
分布，F分布についての検定統計量があるとすると，
値は適切な 
値関数を使って計算することができる．例えば，NormalPValueではゼロ平均で単位分散の正規分布を使った検定統計量に対する 
値を計算するのに使われる．両側 
値はTwoSided->Trueと設定することで得ることができる．
| NormalPValue[teststat] | 平均0で単位分散を持つ正規分布について teststat の  値を与える |
| StudentTPValue[teststat,dof] | 自由度 dof のスチューデントの t 分布について teststat の  値を与える |
| ChiSquarePValue[teststat,dof] | 自由度 dof の  分布について teststat の  値を与える |
| FRatioPValue[teststat,numdof,dendof] | 分子自由度が numdof，分母自由度が dendof であるF分布について teststat の  値を与える |
信頼区間
信頼区間は，あるパラメータが一定の確率で含まれる範囲を与える．パラメータの区間推定は，問題のパラメータについての統計的推測においてのみでなく，推定量の確度の観測においても有用なことがよくある．
MeanCIとMeanDifferenceCIは中心極限定理(Central Limit Theorem)に基づいて平均および平均の差分の信頼区間を与える．
| MeanCI[list] | list から推定された母平均に対する信頼区間を与える |
| MeanDifferenceCI[list1,list2] | list1と list2から推定された母平均間の差分に対する信頼区間を与える |
データが抽出された母集団の分散についての仮定は，パラメータ推定値の分布に影響を及ぼす．オプションKnownVarianceとEqualVariancesは母分散についての仮定を指定するために使うことができる．
オプション名
|
デフォルト値
| |
| KnownVariance | None | 既知の母分散の値 |
MeanCIとMeanDifferenceCIのオプション
平均および平均間の差分に対する信頼区間は，母分散が既知であると仮定される場合は正規分布に基づく．
母分散を 
個の要素のリストから想定しなければならない場合は，平均に対する区間は自由度 
のスチューデントの 
分布に基づく．
オプション名
|
デフォルト値
| |
| EqualVariances | False | 未知の母分散が等価であると仮定するかどうか |
MeanDifferenceCIのオプション
平均間の差分に対する信頼区間も，分散が既知でなければスチューデントの 
分布に基づく．分散が等しいと想定されるときは，MeanDifferenceCIは自由度Length[list1]+Length[list2]-2のスチューデントの 
分布に基づく．母分散が等しいと想定されない場合は，自由度についてウェルチの近似が使われる．
VarianceCIとVarianceRatioCIは，正規分布に従う標本の分散のテストを行う．
| VarianceCI[list] | list から推定された母分散に対する信頼区間を与える |
| VarianceRatioCI[list1,list2] | list1と list2から推定された母分散の比に対する信頼区間を与える |
信頼区間関数でのデフォルトの信頼水準は.95である．他の水準はConfidenceLevelオプションで指定できる．
オプション名
|
デフォルト値
| |
| ConfidenceLevel | .95 | 区間に対する信頼水準 |
平均の推定値，分散あるいは分散比，必要な標準偏差か自由度が与えられても，正規分布，カイ二乗分布，スチューデントの 
分布，F分布の信頼区間が得られる．
| NormalCI[mean,sd] | 中心が mean で標準偏差が sd の信頼区間を与える |
| StudentTCI[mean,se,dof] | 中心が mean，標準誤差が se，自由度が dof の信頼区間を与える |
| ChiSquareCI[variance,dof] | 標本分散が variance で自由度が dof のときの母分散の信頼区間を与える |
| FRatioCI[ratio,numdof,dendof] | 標本分散の比が ratio で，分子と分母の標本分散の自由度がそれぞれ numdof，dendof であるときの母分散比の信頼区間を与える |