MultivariateStatistics`
MultivariateStatistics`

WishartDistribution

WishartDistribution[Σ,m]

スケール行列Σ，自由度パラメータ m のウィッシャート(Wishart)分布を表す．

詳細とオプション

  • WishartDistributionを使うためには，まず多変量統計パッケージをロードしなくてはならない．それにはNeeds["MultivariateStatistics`"]を実行する必要がある．
  • ウィッシャート分布の対称正定値行列 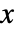の確率密度は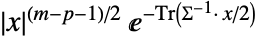，に比例する．
  • スケール行列Σは任意の対称正定値行列になり得る．パラメータ m は m>Length[Σ]となるような任意の数になり得る．
  • 整数 m のとき，ウィッシャート分布は多変量正規標本の共分散行列の分布を与える．
  • WishartDistributionはMean，PDF，RandomReal等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

ウィッシャート分布の平均：

分散：

確率密度関数：

スコープ  (3)

ウィッシャート分布に従う擬似乱数行列集合を発生させる：

考えられる問題  (2)

WishartDistributionはΣが対称の正定値行列でない場合は定義されない：

WishartDistributionは m<Length[Σ]のときは定義されない：

無効なパラメータを記号的出力に代入すると，意味をなさない結果となる：

Wolfram Research (2007), WishartDistribution, Wolfram言語関数， https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html.

テキスト

Wolfram Research (2007), WishartDistribution, Wolfram言語関数， https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html.

CMS

Wolfram Language. 2007. "WishartDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html.

APA

Wolfram Language. (2007). WishartDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html

BibTeX

@misc{reference.wolfram_2024_wishartdistribution, author="Wolfram Research", title="{WishartDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_wishartdistribution, organization={Wolfram Research}, title={WishartDistribution}, year={2007}, url={https://reference.wolfram.com/language/MultivariateStatistics/ref/WishartDistribution.html}, note=[Accessed: 22-November-2024 ]}