Notation，Symbolize，InfixNotation

NotationInfixNotation
Symbolize表記法の入力

Notation

Notation[boxes ⟺ expr]boxes が expr に構文解析され，expr が boxes としてフォーマットされるよう設定する
Notation[boxes ⟹ expr]boxes が expr と構文解析されるように設定する
Notation[boxes ⟸ expr]expr が boxes としてフォーマットされるよう設定する
Notation[notation, opts]オプション opts を伴う表記法 notation を定義する
RemoveNotation[notation]表記法 notation を削除する

表記法の宣言のシンタックス

Notationは引数として外部表現と内部表現の両方を取る．Wolfram言語は外部表現に合致する入力すべてを対応する内部表現に変換し，また反対に，内部表現に合致する式を対応する外部表現にフォーマットする．ここで表現というのは，ある「表記法」を表すボックスで構成された複合構造のことである．

パッケージをロードする．
gplusという新しい表記法を宣言する．
x_ ⊕n_ y_に合致する入力はすべてgplus[x,y,n]として構文解析される．
gplus式はすべて新しい表記法にフォーマットされる．

⟺を使って定義された表記法は，指定の表記法に従って式を構文解析・フォーマットする．しかし，表記法の命令文の中で⟺の代りに⟹または⟸を使って，このような表記法を構文解析だけ，またはフォーマットだけするように限定することもできる．

仮のDomainIntegralの構文解析のための表記法を定義する．
これでDomainIntegralが解析可能になった．
外観がより従来の数式に近いDerivativeオブジェクトの出力形式を定義する．
これにより，導関数は新しい導関数表記法でフォーマットされる．
前の出力を入力として使えるようにするために，偏導関数の構文解析が定義できる．
これでこれらの新しい導関数の表記法が使えるようになった．

ユーザは通常構文解析とフォーマットの両方の機能が使用できると考えているので，両方の表記法の定義を行うことが望ましい．

次の表記法は，Applyが上ルビとして付加された矢印のフォーマットと構文解析をするものである．
線形性など簡単な規則が，直観的な方法で入力できるようになった．

初めはNotation文の両辺のアンダースコアがいくらか奇異に感じるかもしれない．しかし，表記法の変換は通常双方向に機能するため，Notation文の両辺のアンダースコアは至極自然なものであり，すぐに直観的に理解できるようになるであろう．

Symbolize

Symbolize[boxes]boxes をシンボルとして扱う
Symbolize[boxes,opts]boxes をオプション opts を伴うシンボルとして扱う
RemoveSymbolize[boxes]boxes をシンボルとして扱うことを中止する

シンボル化の宣言のシンタックス

Symbolizeはボックス構造のクラスを内部的にシンボルとして扱うために使われる．複合オブジェクトは，ときにシンボル化しなければならないことがある．例えば複合オブジェクトに規則が付加できるようにするためには，そのオブジェクトはシンボルとして扱われなければならない．

次の式は複合オブジェクトℴ∂ がシンボルとして扱われるように宣言する．
パッケージは複合シンボルℴ∂ 用のFullForm名を作成した．
これで複合シンボルℴ∂ に規則が添付できるようになった．
上記のℴ∂ の規則はDomainIntegralの規則の前に適用が試みられる．
Symbolizeは，例えばRuleが下付き文字として付加されているオブジェクトすべてをシンボル化するために，式のクラスもシンボル化する．
これでRuleが下付き文字として付加されているものはすべてシンボルとして扱われるようになった．

シンボル化されたボックス構造は，定義の中でパターン変数として使うことができる．これにより，より親しみやすい表記法で公式が作成できる．しかし，「複合パターン変数:パターンの内容」の形のパターン式を使わなければならない．この形でないと，Wolfram言語がそのパターン式を「複合パターン変数*パターンの内容」と構文解析してしまうことがある．

次の式は，ある状況下でのポテンシャルステップにおける入射波パケットの透過係数を定義する．

InfixNotation

InfixNotation[op,func]op を関数 func を表す中置演算子として扱う
InfixNotation[op,func,opts]op をオプション opts を伴う関数 func を表す中置演算子として扱う
RemoveInfixNotation[op,func]複合中置演算子 op を削除する

中置表記法の宣言のシンタックス

InfixNotationは複合ボックス構造を挿入演算子として扱うために用いられる．InfixNotationは挿入演算子を表す複合ボックスオブジェクトと，式の完全形頭部となるシンボルの両方を必要とする．この双対性は，Wolfram言語において挿入表記法+が完全形頭部Plusを持っているのと類似している．

複合オブジェクト+{}がJoinの挿入形式として動作するように宣言する．
挿入表記法+{}は入力を構文解析し，出力をフォーマットする．

挿入演算子の定義にNotationではなくInfixNotationを使うと，式を評価することなく内部のフラットな形式に構文解析できるという利点がある．これは小さなことではあるが，重要である（リング演算，可能な限り評価せずに構文解釈するを参照のこと）．

InfixNotationは入力を構文解析してフラットな式にする．

関数InfixNotationは，関数~f~の挿入形式を使用する場合と比較できる（「式の特殊な入力法」を参照のこと）．

表記法の入力

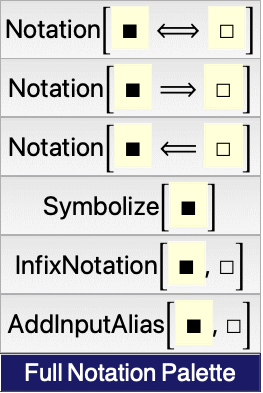
独自の表記法の定義の際には，表記法テンプレートを使うことが「非常に」重要となる．表記法テンプレートは以下に示される表記法パレットに含まれている．

1.gif

このような制限があるのは，ノートブックにペーストされたテンプレートには基本的なタグボックスが正しく埋め込まれているからである．このような埋め込まれたタグボックスを利用すると，Notation，Symbolize，InfixNotationを使って新しく定義される表記法を適切にグループ化し，構文解析することができるようになる．さらに，これらの関数も新しい表記法のスタイル情報を得て，出力が入力と同じスペーシング，サイズ，調整などでフォーマットできるようになる．

空の表記法テンプレートは次のようなものである．

注：表記法パレットを使わないで，対応する文字のボックス構造をParsedBoxWrapperで囲んでもよい．

Wolfram言語では，必要な表記法や式すべてについて入力エイリアスが作成できる．このような入力に使う通常のインターフェースはやや扱いにくいため，表記法パッケージには関数AddInputAliasが含まれている．これは現行のノートブックに容易に入力エイリアスが加えられるようにするためのものである．一般的なテンプレートには簡単に入力するためのそれぞれのエイリアスがある．例えばEsc notation Escと入力すると，表記法テンプレートNotation[ ⟺ ]が入力される．

現行ノートブックに命令文を適用するための入力エイリアスを加える．

これでEsc apply Escと入力するだけで「適用」テンプレートが入力できるエイリアスが作成された．