WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

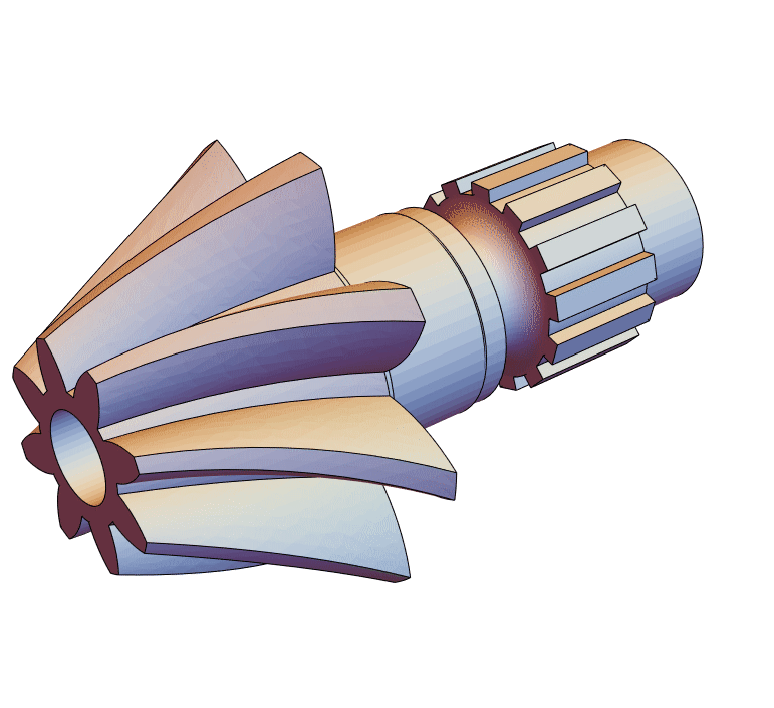
Helical Bevel Gear

The purpose of this tutorial is to illustrate the usage of the OpenCascadeLink to greate a helical bevel gear. The shape and the procedure of the creation are based on a computer aided design (CAD) tutorial [1].

1.gif

The creation of the gear will be done in several stages. First, the shaft is created. As a second step the gear will be made. Both the shaft and the gear will be combined. Following that the bosses are added and lastly the gear will be perforated.

Load the packages.
In[1]:=1
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-8bxqkz

Shaft

The shaft will be created by specifying a cross section in the X-Z plane. This cross section will then serve as a basis for a solid created from a revolution around the X-axis.

2.gif

The cross section will consist of three parts, two line segments and a half circle.

Specify a cross section of the shaft:
In[10]:=10
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-swzasa

Note that the orientation of the segments is important. Should the orientation of the segments in the opposite direction the revolution will result in a solid that specifies the region outside of the shaft. If the orientation of a set of segments be in the opposite direction to what is wanted a trick is to revert the axis of revolution in the exact opposite direction. That will avoid respecifying the segments too.

Specify the cross section:
In[15]:=15
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-tu0gck
Visualize the cross section of the shaft:
In[16]:=16
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-behyp6
Out[16]=16
Create OpenCascade objects from the cross section:
In[17]:=17
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-3jbm24
Out[17]=17
Combine the segments into a single wire object
In[18]:=18
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-dr59bv
Out[18]=18
Out[19]=19

While OpenCascadeShapeUnion could have been used to combine the segments into a single object, OpenCascadeShapeUnion will return a compound and it’s harder to see what is in a compound.

Next, the cross section will be revolved around a rotation axis along the X-axis.

Create a rotation axis:
In[20]:=20
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-858ye6
Out[21]=21
Create the rotational sweep of the cross section around the rotation axis:
In[22]:=22
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-n9g4jo
Out[22]=22
Inspect the type of the shape object created:
In[23]:=23
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-18l8u
Out[23]=23

Now that the cross section is rotated the resulting shape is a shell. That is because the input to the rotation was a wire. However, we would like to have a solid.

Create a solid from the shell and inspect the type:
In[24]:=24
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-87gyzu
Out[24]=24
Out[25]=25

As an alternative, one could have used Polygon for the creation of the cross section. These are face type OpenCascade objects and after a revolution would have returned an OpenCascade solid.

Extract a boundary element mesh:
In[26]:=26
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-6zb00y
Out[26]=26
Visualize the boundary element mesh of the shaft:
In[27]:=27
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-tsoeqz
Out[27]=27

To verify that the boundary mesh construction worked as intended, a full element mesh is generated.

Create a full element mesh:
In[28]:=28
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-n03yb6
Out[28]=28

The warning message will disappear if the boundary element mesh is created with a smaller "LinearDeflection" value than the default.

Gears

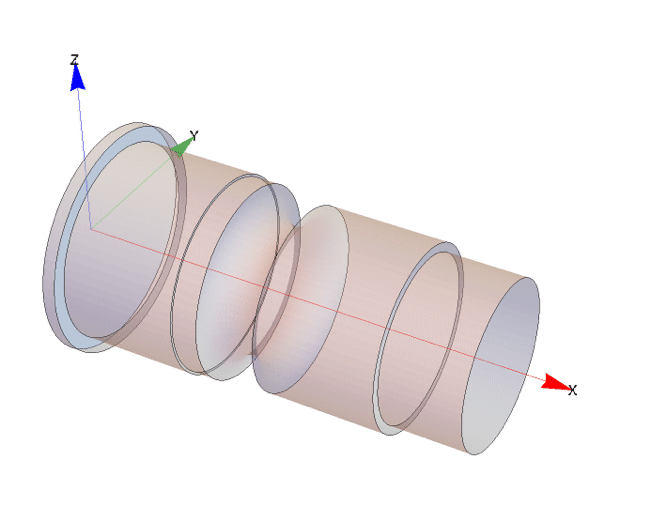
The creation of the gear itself will be done in two steps. First half a gear tooth is modeled in the YZ-plane. The half tooth is constructed by combining three sections of circles. This half tooth is then mirrored at an axis to give a complete tooth. The the single tooth is rotated to make a set of gear teeth in the YZ-plane. Once that is done the gear in the YZ-pane is translated, rotated and scaled in a second plane parallel to the YZ-plane. This procedure is repeated one more time to give a third set of teeth in a third plane again parallel to YZ-plane. The actual gear is then created by extruding through the planes. This created a loft.

4.gif

Gear teeth

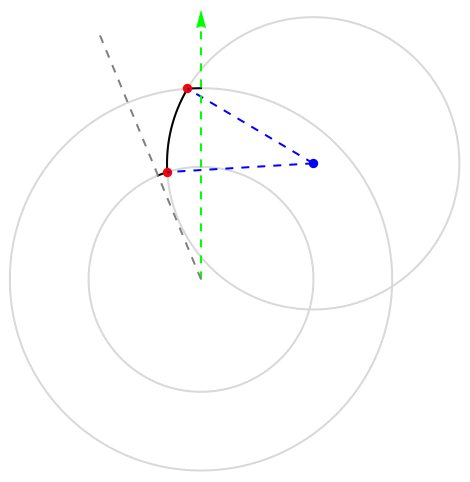
The gear tooth will be created by intersecting three circles and taking parts of their boundaries.

5.gif

We start by sketching the procedure of the gear tooth generation in 2D.

Define different radii:
In[29]:=29
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-wlkx0t
Specify the intersection points:
In[32]:=32
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-5iux0k
Out[32]=32
Out[33]=33
Find the coordinate of the third circle such that is passes through the specified intersection points and has the given radius r3:
In[34]:=34
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-7muefw
Out[35]=35
Visualize the three circles and the relevant intersections.
In[36]:=36
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-gklhqr
Out[36]=36
Compute the arc angles for the circles from p3:
In[37]:=37
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-6865sc
Out[37]=37
Out[38]=38
Visualize the circle arcs that make half a gear tooth:
In[39]:=39
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-yh9u24
Out[39]=39
Mirror the half tooth and rotate the tooth for a full set of gears:
In[45]:=45
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-1azniw
Out[49]=49

Next, we proceed to put the above insight into 3D. Since the Wolfram language does not have a Circle primitive that can be used in 3D OpenCascadeLink provides one. The primitive allows one to specify coordinates through which the circle should pass.

Compute the end point of the third arc.
In[50]:=50
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-lvwv2l
Out[50]=50
Setup the OpenCascade 3D Circle primitives:
In[51]:=51
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-0ngc5d
Create OpenCascade shape objects:
In[54]:=54
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-d12yum
Make a single wire from the arc segments:
In[55]:=55
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-nojk89
Out[55]=55
Inspect the resulting type:
In[56]:=56
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-sl212v
Out[56]=56

Next, the half tooth is mirrored along the Z-axis.

Set up a rotation transform in the Z-axis direction:
In[57]:=57
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-cl56at
Out[57]=57
Create the full gear tooth by combining the half tooth and the mirrored half tooth:
In[58]:=58
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-4scm4q
Out[58]=58
Set up a rotation transforms in steps of of 2π/8 in the X-axis direction
In[59]:=59
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-dy3dpt
Create the gear profile wire in the YZ-axis by multiple rotations of the single tooth around the X-axis:
In[60]:=60
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-or6qlv
Out[60]=60

To visualize the created gear profile in 3D we use a trick to give the flat profile an extension in the X-direction. This is purely for visualization and is not needed for the gear constriction.

Visualize the gear profile in 3D together with the shaft:
In[61]:=61
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-oheoqc
Out[62]=62

Make planes

Now, the the gear profile is created that profile can be scaled, rotated and translated to create the gear profiles parallel to each other in the YZ-plane.

Create the second gear profile:
In[63]:=63
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-j7fbg2
Create the third gear profile:
In[66]:=66
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-cdsoeb
Visualize the gear profiles:
In[69]:=69
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-vt9l6z
Out[70]=70
Construct the full 3D gear by creating surfaces through the gear profiles in the YZ-panes:
In[71]:=71
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-z2kh5n
Out[71]=71
Extract a boundary element mesh:
In[72]:=72
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-dbmwi
Visualize the boundary element mesh of the gear:
In[73]:=73
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-re1w5e
Out[73]=73

To verify that the boundary mesh construction worked as intended, a full element mesh is generated.

Create a full element mesh:
In[74]:=74
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-6jmyk8
Out[74]=74

Combine

The shaft and the gear are now combined.

Create the union of the shaft and the gear.
In[75]:=75
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-32ee9p
Out[75]=75
Extract a boundary element mesh:
In[76]:=76
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-cg6syl
Visualize the boundary element mesh of the union of the shaft and the gear:
In[77]:=77
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-it57eg
Out[77]=77

To verify that the boundary mesh construction worked as intended, a full element mesh is generated.

Create a full element mesh:
In[78]:=78
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-o0ub0j
Out[78]=78

Boss

Create a Cuboid that will be used to make the bosses:
In[79]:=79
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-mksaq1
Out[79]=79
Visualize the beveled gear and a single boss:
In[80]:=80
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-s34deq
Out[80]=80
Verify the the boss does indeed intersect the surface of the shaft properly:
In[81]:=81
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-6ttbpf
Out[81]=81
Create 13 bosses:
In[82]:=82
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-virn66
Form the union of the bosses with the beveled gear:
In[85]:=85
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-44pcto
Out[85]=85
Extract a boundary element mesh:
In[86]:=86
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-0glinr
Visualize the boundary element mesh of the union of the shaft and the gear:
In[87]:=87
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-q97phh
Out[87]=87

To verify that the boundary mesh construction worked as intended, a full element mesh is generated.

Create a full element mesh:
In[88]:=88
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-pshy3o
Out[88]=88

Hollow shaft

Create a Cylinder to use to perforate the object:
In[89]:=89
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-lvgzl1
Out[89]=89
Visualize the beveled gear and the cylinder that is to create the perforation:
In[90]:=90
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-15g4tv
Out[90]=90
Create the difference of the beveled gear and the cylinder:
In[91]:=91
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-u093y4
Out[91]=91
Extract a boundary element mesh:
In[92]:=92
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-chl2nq
Visualize the boundary element mesh of the union of the shaft and the gear:
In[93]:=93
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-de67wz
Out[93]=93

To verify that the boundary mesh construction worked as intended, a full element mesh is generated.

Create a full element mesh:
In[94]:=94
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-eccdab
Out[94]=94
Extract a boundary element mesh with a refined surface approximation:
In[95]:=95
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-45vw9p
In[97]:=97
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-wytfyn
Out[97]=97
Create a full mesh and visualize the beveled gear:
In[100]:=100
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-t05h1f
Out[101]=101

Initialization

The following helper function is to visualize circles in 3D space.

In[1]:=1
✖
https://wolfram.com/xid/0b5g0r5a5qn4smigfjqtkrh0bv5uj5nm-2ny5x1

References

[1] https://www.youtube.com/watch?v=VihInzgm0QA