Electric Motor Noise Analysis
| Introduction | Model without a Sound Barrier |
| Pressure Acoustics Model | Model with a Sound Barrier |
| Domain | Nomenclature |
| Boundary Conditions |
Introduction
Noise analysis is an important phase when designing electrical motor–driven systems. As a motor rotates, the harmonic electromagnetic forces between the rotor and stator continuously deform the outer casing of the motor. These periodic deformations lead to structural vibrations, which excite pressure waves to the surroundings as a noise.
The following model simulates the acoustic wave radiation from a motor spinning at ![]() ,
, ![]() and
and ![]() . First, the sound pressure level (SPL) in the surrounding field is computed to quantify the noise generation. In a subsequent step, a sound barrier will be placed in the domain to reduce noise in a specific direction. The resulting sound pressure field will then be compared to the free-space case to measure the effectiveness of the sound barrier.
. First, the sound pressure level (SPL) in the surrounding field is computed to quantify the noise generation. In a subsequent step, a sound barrier will be placed in the domain to reduce noise in a specific direction. The resulting sound pressure field will then be compared to the free-space case to measure the effectiveness of the sound barrier.
A related example that simulates the magnetic potential and the magnetic flux field within the electric motor is presented in a separate tutorial entitled "Solving Partial Differential Equations with Finite Elements".
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
As a theoretical background for acoustics, please refer to the information provided in "Acoustics in the Frequency Domain".
Pressure Acoustics Model
To model the time-harmonic deformation of the electrical motor, the acoustic model is built in the frequency domain. The propagation of harmonic sound waves can be described by the source-free Helmholtz partial differential equation (PDE) (1):
Domain
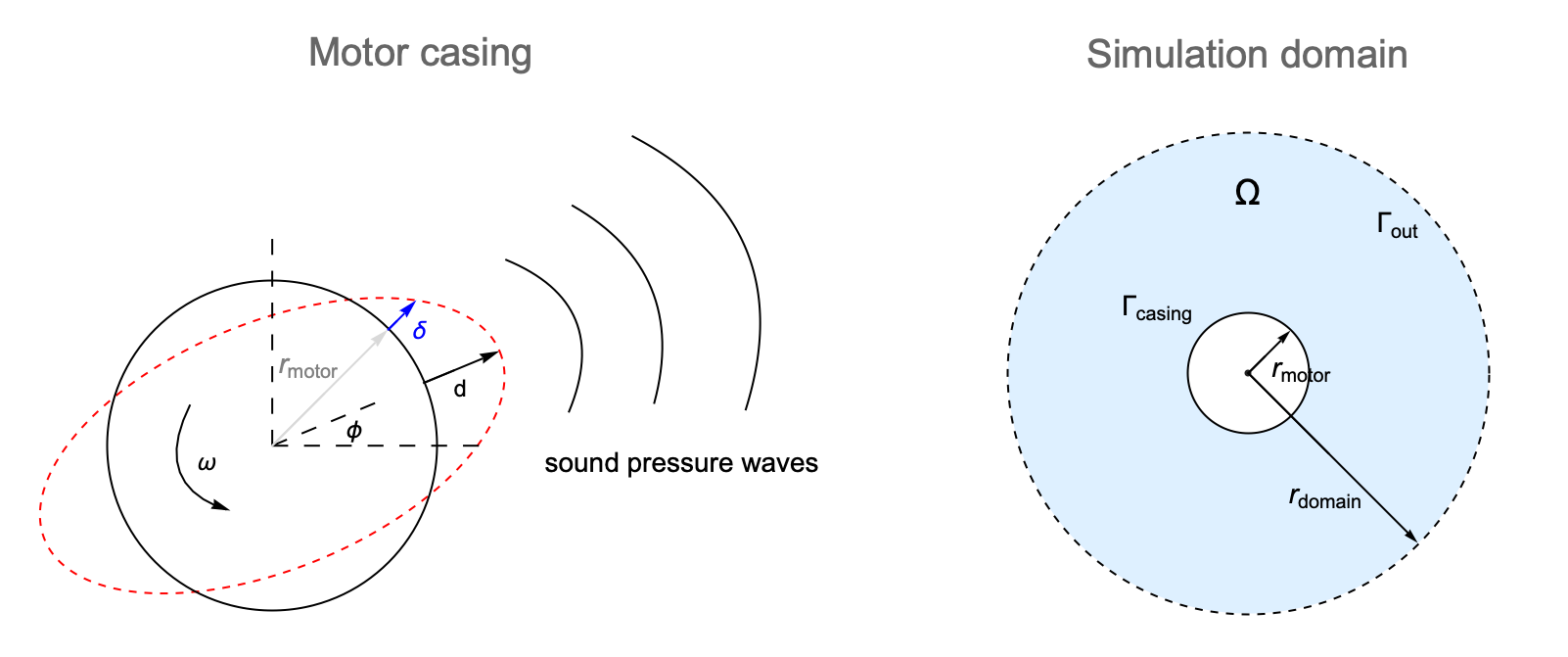
Consider the motor spinning at an angular frequency ![]() : the magnetic forces between the rotor and stator will continuously deform the outer casing of the motor. This periodic deformation
: the magnetic forces between the rotor and stator will continuously deform the outer casing of the motor. This periodic deformation ![]() can be approximately described by the cosine function:
can be approximately described by the cosine function:
In this model, the maximum radial deformation of the motor is set as ![]() . Note that
. Note that ![]() is assumed to be independent of the motor speed
is assumed to be independent of the motor speed ![]() . This is a reasonable approximation, since the eigenfrequencies of the motor are packed so closely in the high-frequency range and have little impact on the structural deformation.
. This is a reasonable approximation, since the eigenfrequencies of the motor are packed so closely in the high-frequency range and have little impact on the structural deformation.
More information on eigenfrequency analysis can be found in the "Acoustics in the Frequency Domain" tutorial.
The polar angle ![]() is defined as the angle measured from the
is defined as the angle measured from the ![]() axis to the point on the motor casing:
axis to the point on the motor casing:
To analyze the noise propagation in the surrounding area, the simulation domain ![]() is defined as a circular region enclosing the electric motor. The radius of the motor and the domain are
is defined as a circular region enclosing the electric motor. The radius of the motor and the domain are ![]() and
and ![]() , respectively. The far-field boundary and the motor casing are symbolized as
, respectively. The far-field boundary and the motor casing are symbolized as ![]() and
and ![]() , respectively.
, respectively.
In acoustics simulations, the wavelength ![]() of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here the max edge length is set to 12 nodes per
of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here the max edge length is set to 12 nodes per ![]() , which means that there will be at least 12 elements per wavelength
, which means that there will be at least 12 elements per wavelength ![]() in each direction of the wave propagation.
in each direction of the wave propagation.
More information on mesh size requirements for acoustic models can be found in the "Acoustics in the Frequency Domain" tutorial.
Boundary Conditions
There are two types of boundary conditions involved in this example. On the motor casing ![]() , a normal velocity boundary condition is used to model the structural vibration.
, a normal velocity boundary condition is used to model the structural vibration.
Recall that the deformation of the casing is approximately described by a cosine function as:
For analytical convenience, equation (2) is converted into the complex exponential representation (CER):
The corresponding vibration velocity ![]() and the velocity amplitude
and the velocity amplitude ![]() are given by:
are given by:
On the far-field boundary ![]() , an absorbing boundary condition is used to truncate the domain
, an absorbing boundary condition is used to truncate the domain ![]() as if it had an infinite extension.
as if it had an infinite extension.
Model without a Sound Barrier
The first goal is to solve for the sound pressure field without any sound barrier.
To visualize the acoustic wave propagation around the motor, the solution is transformed into the time domain with the harmonic wave relation (3):
More information on the relation between time domain and frequency domain can be found here.
See this note about improving the visual quality of the animation.
The acoustic wave radiates from the motor and propagates to the surrounding area in a spiral pattern. A plot of the sound pressure level (SPL) of the domain can be used to inspect the noise distribution. The noise level at distances of ![]() ,
, ![]() and
and ![]() is shown as an SPL polar plot.
is shown as an SPL polar plot.
The SPL value is seen to be at the maximum around the motor casing and decays isotropically with the distance from the motor. Note that the noise level increases with higher motor speed.
The noise level can also be expressed in decibels by the following unit conversion:
where ![]() is the standard reference sound pressure and is commonly chosen as 20 micropascals in air.
is the standard reference sound pressure and is commonly chosen as 20 micropascals in air.
The noise level at ![]() increases with the motor speed and reaches
increases with the motor speed and reaches ![]() at
at ![]() . This is comparable to the noise of a jet engine.
. This is comparable to the noise of a jet engine.
Model with a Sound Barrier
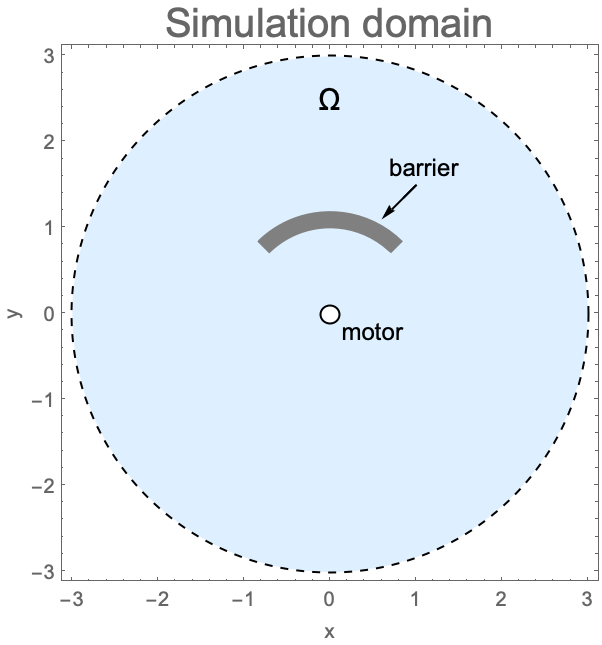
Next, a sound barrier is added in the domain to reduce the motor noise in a particular direction. The barrier is placed at ![]() to minimize the noise in the
to minimize the noise in the ![]() direction.
direction.
In this model, the sound barrier is assumed to be made of a sound hard material, which allows it to reflect the incident sound waves. A sound hard boundary condition, which is an implicit default boundary condition, will be used to model the boundary of the barrier.
See this note about improving the visual quality of the animation.
Note that the noise level is significantly reduced in the ![]() direction between
direction between ![]() to
to ![]() for all three motor speeds. However, on the opposite region, the noise level is increased, due to the sound reflection from the barrier.
for all three motor speeds. However, on the opposite region, the noise level is increased, due to the sound reflection from the barrier.
Nomenclature
| Symbol | Description | Unit |
| R | revolutions per minute in a motor | [rad/s] |
| ρ | density of a medium | [kg/m3] |
| c | speed of sound in a medium | [m/s] |
| p | sound pressure | [Pa] |
| ω | sound wave angular frequency | [rad/s] |
| f | sound wave frequency | [Hz] |
| λ | sound wavelength | [m] |
| X | position vector | [m] |
| rmotor | radius of the motor | [m] |
| rdomain | radius of the domain | [m] |
| δ | deformation of the motor casing | [m] |
| d | maximum radial deformation | [m] |
| ϕ | polar angle | [rad] |
| Γout | far-field boundary | N/A |
| Γcasing | motor casing | N/A |
| v | vibration velocity | [m/s] |
| vibration amplitude | [m/s] | |
| Ω | computational domain | N/A |