Eigenfrequencies of a Room
| Introduction | Post-processing and Visualization |
| Eigensystem Acoustic Model | Analytical Eigenfrequencies/Eigenmodes of the Empty Room |
| Domain | Nomenclature |
| Boundary Conditions | References |
| Solve the PDE Model |
Introduction
Acoustic resonance is a phenomenon arising when an object subjected to relatively small sound waves greatly amplifies the sound waves. This resonance appears when the frequency of a stimulus matches one of the natural frequencies (i.e. eigenfrequencies) of the object. When in resonance, the amplitudes of vibration tend to be much larger, so when objects vibrate at their eigenfrequencies, they are more subject to fatigue and breakage. For example, a delicate wineglass can be broken when induced to vibrate at its natural frequencies. Eigenfrequency analysis is an important consideration when designing acoustic systems that utilize (or prevent) resonance, such as musical instruments, acoustic filters and concert halls.
As a demonstration, consider a rectangular ![]() ×
×![]() ×
×![]() room model with some furniture in it. The first five eigenfrequencies are sought numerically and will be compared with the analytical eigenfrequencies of a room without furniture. The corresponding eigenmode at each eigenfrequency will then be visualized to show the resonant sound field of the room.
room model with some furniture in it. The first five eigenfrequencies are sought numerically and will be compared with the analytical eigenfrequencies of a room without furniture. The corresponding eigenmode at each eigenfrequency will then be visualized to show the resonant sound field of the room.
The symbols and corresponding units used here are summarized in the Nomenclature section.
Please refer to the information provided in "Acoustics in the Frequency Domain" for more general theoretical background for acoustics.
Eigensystem Acoustic Model
Eigenfrequency analysis is done with a frequency domain model. In the frequency domain, the sound pressure field ![]() of an acoustic system is described by the Helmholtz partial differential equation (PDE):
of an acoustic system is described by the Helmholtz partial differential equation (PDE):
where the terms ![]() and
and ![]() are monopole and dipole sources, respectively.
are monopole and dipole sources, respectively.
Since there is no sound source in this room model, equation (1) simplifies to the source-free Helmholtz equation:
To solve for the eigenfrequency ![]() and the eigenmode
and the eigenmode ![]() of the room, equation (2) is treated as an eigenvalue problem such that
of the room, equation (2) is treated as an eigenvalue problem such that ![]() and is solved with NDEigensystem. Here, the differential operator
and is solved with NDEigensystem. Here, the differential operator ![]() corresponds to the left-hand side of (3), and
corresponds to the left-hand side of (3), and ![]() represents the eigenvalue of the eigensystem.
represents the eigenvalue of the eigensystem.
The set of eigenvalues ![]() that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies
that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies ![]() by:
by:
Domain
The room model has a length of ![]() , a width of
, a width of ![]() and a height of
and a height of ![]() . Furniture such as a sofa, a coffee table and a television are put in the room to form a simple living room. All boundaries, including walls, furniture and floor, are assumed to be solid and are modeled with sound hard boundary conditions.
. Furniture such as a sofa, a coffee table and a television are put in the room to form a simple living room. All boundaries, including walls, furniture and floor, are assumed to be solid and are modeled with sound hard boundary conditions.
This room model, however, cannot be directly applied in the acoustic simulation, since it represents the boundary of the simulation domain ![]() . The actual acoustic simulation domain
. The actual acoustic simulation domain ![]() is the space that is filled with the sound medium (i.e. air) within the room.
is the space that is filled with the sound medium (i.e. air) within the room.
A predefined boundary mesh that resembles the space occupied by the air is available and can be imported.
In acoustics simulations, the wavelength ![]() of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here, the max edge length is set to 12 nodes per
of a sound wave needs to be resolved by a sufficiently fine mesh in order to get an accurate numerical solution. Here, the max edge length is set to 12 nodes per ![]() , which means that there will be at least six elements per wavelength
, which means that there will be at least six elements per wavelength ![]() in each direction of the wave propagation.
in each direction of the wave propagation.
More information on mesh size requirements for acoustic models can be found in the "Acoustics in the Frequency Domain" tutorial.
Boundary Conditions
Since all the boundaries of the room are assumed to be perfectly rigid, the only boundary condition involved in this model is the sound hard boundary condition.
Note that the sound hard boundary condition is essentially a Neumann zero boundary, which means it is implicitly used by default if no other boundary condition is specified at a given boundary.
Solve the PDE Model
To analyze the acoustic behavior of the room model, the first five eigenvalue/eigenfunction pairs are solved for with NDEigensystem.
Post-processing and Visualization
Eigenfrequencies of the Furnished Room
Recall that the set of eigenvalues ![]() that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies
that fulfills the source-free Helmholtz equation gives the corresponding eigenfrequencies ![]() by:
by:
Note that the gap between two consecutive eigenfrequencies decreases in a higher frequency range.
Eigenmodes of the Furnished Room
The next step is to visualize the resonant sound field in the furnished room. The sound pressure field ![]() that is paired with each eigenfrequency
that is paired with each eigenfrequency ![]() is called the room eigenmode.
is called the room eigenmode.
See this note about improving the visual quality of the animation.
As shown in the acoustics time domain tutorial, the locations where the sound pressure reaches its local maximum are called the antinodes of an acoustic system. A sound source at these points will excite the sound field the most, which makes them ideal places to put the loudspeakers.
Analytical Eigenfrequencies/Eigenmodes of the Empty Room
As a comparison, the analytical eigenfrequencies for the room without furniture can be used. The eigenfrequencies in an empty rectangular (![]() ) room can be computed by the formula [4]:
) room can be computed by the formula [4]:
The mode index ![]() ,
, ![]() ,
, ![]() is a positive integer triple. Each unique combination of the mode index determines a specific eigenfrequency of the room.
is a positive integer triple. Each unique combination of the mode index determines a specific eigenfrequency of the room.
In this case, the first five eigenfrequencies of the empty room model correspond to the mode indices: ![]() .
.
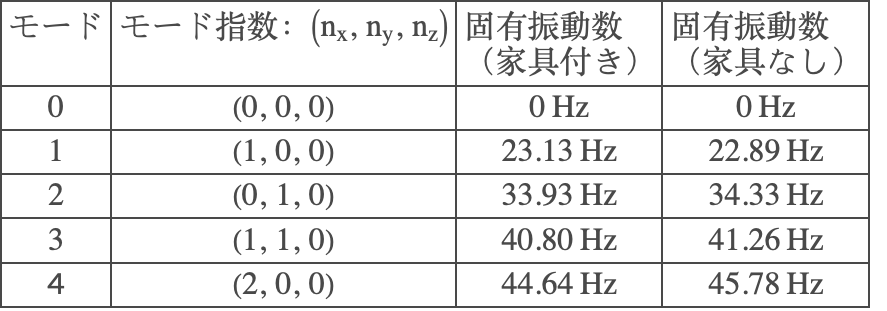
The following table summarizes the first five eigenfrequencies of the furnished room and the empty room. By convention, the first nonzero eigenfrequency is denoted as mode 1 and is called the fundamental frequency or the first harmonic of the room.
For the first five modes, the eigenfrequencies of the furnished room are very close to the empty room. That is, in a low-frequency range, the furniture has little impact on the room eigenfrequencies.
The analytical eigenmodes ![]() of the empty room are given by the formula [5]:
of the empty room are given by the formula [5]:
where ![]() is an arbitrary constant.
is an arbitrary constant.
See this note about improving the visual quality of the animation.
The effect of the furniture can be seen by comparing eigenmodes between the empty room and the furnished room (shown in the previous section). For example, at mode 4, the sofa breaks the evenly distributed sound field of the empty room and confines the maximum sound pressure behind it.
Nomenclature
| Symbol | Description | Unit |
| ρ | density of a medium | [kg/m3] |
| c | speed of sound in a medium | [m/s] |
| p | sound pressure | [Pa] |
| pi | the itheigenmode | [Pa] |
| ω | sound wave angular frequency | [rad/s] |
| f | sound wave frequency | [Hz] |
| fi | the itheigenfrequency | [Hz] |
| F | optional dipole source | [N/m3] |
| Q | optional monopole source | [1/s2] |
| X | position vector | [m] |
| λ | wavelength | [m] |
| h | mesh size | [m] |
| Lx,Ly,Lz | dimension of the room | [m] |
| nx,ny,nz | mode index | N/A |
| Ω | computational domain | N/A |
References
1. Heutschi, K. Lecture Notes on Acoustics I. Swiss Federal Institute of Technology Zurich, 2016.