Biaxial Tensile Test of Hyperelastic Tissue
Introduction
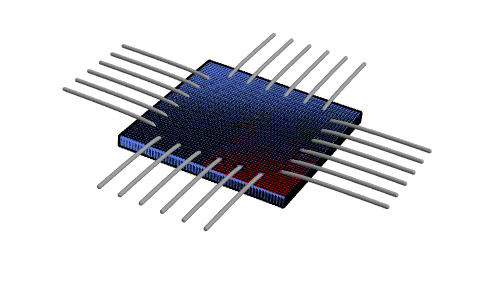
Biaxial tensile testing is an experimental technique to characterize materials. For this purpose, a rectangular material specimen is perforated with holes that act as anchors for hooks. The hooks will be pulled apart, both the forces applied and the resulting displacements measured. An illustration of a specimen pulled with a typical number of hooks is shown below.
Highlighted in red is the symmetry of the setup, which is exploited later in order to reduce computational complexity.
The experimental tools for biaxial tensile testing provide a high measurement resolution and, additionally, the possibility to measure in orthogonal directions, which allows anisotropic material to be characterized. The results from a biaxial tension test can then be used to calibrate a hyperelastic material model. While biaxial tensile testing is not a new technique, applying biaxial tensile testing to biological material is [Fehervary,2016].
The following tutorial implements a finite element simulation of a biaxial test. Biaxial tests are generally used to show anisotropic behavior. To keep things simple, this example uses an isotropic neo-Hookean model. Material parameters for vascular tissue obtained from the literature are used. [Karimi,2013]. This allows the computational results to be compare with experimental results [Zemanek,2008].
2D FEM Model
For the model, a stationary 2D plane stress formulation is used.
A neo-Hookean material model is used, with parameters from literature.
Geometry
Since the specimen and the positioning of the hooks are symmetric, it is sufficient to model a quarter of the specimen using twofold symmetry. The process begins by specifying the length and thickness of the reduced simulation domain, as well as the hole radius.
Model Setup
For this model, two types of boundary conditions are needed: the symmetry conditions to model the reduced simulation domain and boundary conditions to model the pulling of the hooks. For modeling the pulling of the hooks, the goal is to set up a parametric solver with a parametric variable ![]() that is a prescribed displacement. The parameter
that is a prescribed displacement. The parameter ![]() allows the applied forces to slowly be increased, which is needed since the problem is too strongly nonlinear to solve in a single step. For more information, see the section on strongly nonlinear Hypoelastic Models and the Displacement Conditions in the Solid Mechanics monograph.
allows the applied forces to slowly be increased, which is needed since the problem is too strongly nonlinear to solve in a single step. For more information, see the section on strongly nonlinear Hypoelastic Models and the Displacement Conditions in the Solid Mechanics monograph.
First, the symmetry condition is investigated. The symmetry conditions apply at ![]() and
and ![]() , respectively, and the displacement is set to 0 in the respective direction that the other direction left free to move.
, respectively, and the displacement is set to 0 in the respective direction that the other direction left free to move.
For the pulling of the hooks, displacement conditions are used. A total displacement of up to 40% is specified, and the boundary conditions are set accordingly.
The next step is to specify the positions where these hooks are placed. It is assumed that the hooks are rigid and the pulling occurs on the half of the boundary of the holes where the force is applied. To make this easy, a rectangular region is selected around the respective holes.
To make use of these rectangular regions, the RegionMember is used to convert them to predicates suitable for the solid mechanics boundary conditions. The result from RegionMember includes constraints that the numbers must be real. In the finite element simulation, the mesh coordinates are always real, and the constraint can be removed by using Refine.
Since DirichletCondition is only applied at boundaries nodes of the mesh, these predicates now correspond to the semicircles that are the intersection of the blue circles and the colored rectangles, as highlighted in red and green in the figure above.
Note that the value of applied displacement is given via the parameter ![]() . Also note that for the right predicate, a displacement is used such as to be 0.8 times that for the top displacement. For biaxial tension testing, various force configurations are used to measure the material characteristics. Here, a factor of 0.8 has been arbitrarily chosen between the two directions.
. Also note that for the right predicate, a displacement is used such as to be 0.8 times that for the top displacement. For biaxial tension testing, various force configurations are used to measure the material characteristics. Here, a factor of 0.8 has been arbitrarily chosen between the two directions.
Solution
To solve the PDEs with the strong nonlinearity of hyperelasticity, the parametric solver can be used by gradually increasing the displacement in a sufficient number of steps. Furthermore, for each step, the stress-strain relation can be extracted to obtain the final curve describing the tensile test experimental procedure. The averaged Cauchy stress can be used to extract stress and strain.
To reduce the simulation time and memory usage, the strain, stress and stress-strain curve are only computed every 10th step.
Post-processing
After obtaining the solution, the data can be processed to investigate the stress and strain fields within the domain of the sample.
First of all, the stress-strain relation obtained from each step of the parametric solver can be observed and compared with experimental data [Zemanek,2008].
The effect of traction exerted by the hooks in both directions can be observed. The Cauchy stress can be plotted over the stretch, which is related to the engineering strain as ![]() . The hyperelastic material shows a high deformation, up to 40%, and a good correspondence with the experimental data can be observed. The model is very good up to 20% of strain; however, at high deformation starts to deviate from the experimental data. Nevertheless, it remains a good model to describe this vascular tissue, and in order to better fit the data, the material parameters could be optimized, which is outside the scope of this model.
. The hyperelastic material shows a high deformation, up to 40%, and a good correspondence with the experimental data can be observed. The model is very good up to 20% of strain; however, at high deformation starts to deviate from the experimental data. Nevertheless, it remains a good model to describe this vascular tissue, and in order to better fit the data, the material parameters could be optimized, which is outside the scope of this model.
Next, stress and strain can be extracted and plotted over both the original and the deformed mesh.
In order to create an animation of the deformation process, the bounds of the final deformation are computed first. These bounds will then be used as PlotRange bounds, such that all animation frames use the same plot area.
A note about the quality of the visualization: to get high fidelity visualizations comment out the call to Rasterize above.
To analyze the stress and strain fields, these fields need to be extracted from the solution. Once extracted, they can be plotted for further analysis.
You can observe how the sample is stretched. The deformation is more intense in the top holes, as can expected from boundary conditions and observed from the central plot. The shear strain looks almost symmetric, however, it is slightly unbalanced in the ![]() direction, due to the greater deformation.
direction, due to the greater deformation.
To represent the stress field, it is useful to use MPa units. Therefore, the stress values are multiplied by a conversion factor.
The normal stress along the ![]() direction and
direction and ![]() direction can be used, and it reflects the tensile state due to the boundary conditions. It is focused around the area of the holes and appears to be higher in the
direction can be used, and it reflects the tensile state due to the boundary conditions. It is focused around the area of the holes and appears to be higher in the ![]() direction.
direction.
The von Mises stress is a scalar value used to represent the stress state in the material. It is calculated by taking a weighted average of the different components of the stress tensor, as expressed in the Solid Mechanics monograph.
The von Mises stress field is generally homogeneous in the tissue, with higher stresses appearing near the holes. This is related to the traction boundary conditions, which stretch the sample from the holes.
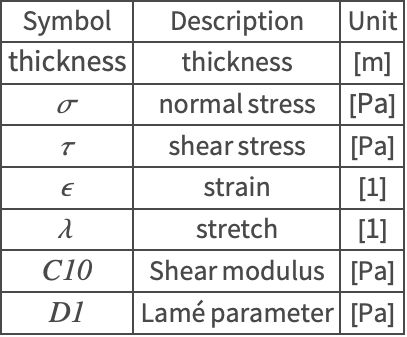
Nomenclature
References
1. H. Fehervary, M. Smoljkić, J. Vander Sloten and N. Famaey (2016). "Planar Biaxial Testing of Soft Biological Tissue Using Rakes: A Critical Analysis of Protocol and Fitting Process." Journal of the Mechanical Behavior of Biomedical Materials, vol. 61, pp. 135–151. https://doi.org/10.1016/j.jmbbm.2016.01.011
2. A. Karimi, M. Navidbakhsh, S. Faghihi, A. Shojaei and K. Hassani (2013). "A Finite Element Investigation on Plaque Vulnerability in Realistic Healthy and Atherosclerotic Human Coronary Arteries." Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 227(2), pp. 148–161. https://doi.org/10.1177/0954411912461239
3. M. Zemánek, J. Bursa and M. Děták. (2008). "Biaxial Tension Tests with Soft Tissues of Arterial Wall." Engineering Mechanics, 16(1) pp. 1–9. https://www.researchgate.net/publication/41842810_Biaxial_Tension_Tests_with_Soft_Tissues_of_Arterial_Wal