AiryBiZero

AiryBiZero[k]

represents the k^(th) zero of the Airy function TemplateBox[{x}, AiryBi].

AiryBiZero[k,x0]

represents the k^(th) zero less than x0.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • N[AiryBiZero[k]] gives a numerical approximation so long as the specified zero exists.
  • AiryBiZero[k] represents the k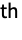^(th) zero less than 0.
  • AiryBiZero can be evaluated to arbitrary numerical precision.
  • AiryBiZero automatically threads over lists. »

Examples

open allclose all

Basic Examples  (4)

Evaluate numerically:

AiryBiZero gives the zeros of AiryBi:

Display zeros of the AiryBi function over a subset of the reals:

Series expansion at Infinity:

Scope  (11)

Numerical Evaluation  (4)

Find the third zero of TemplateBox[{x}, AiryBi]:

Find the second zero of TemplateBox[{x}, AiryBi] less than :

Evaluate numerically to high precision:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix AiryBiZero function using MatrixFunction:

Compute average-case statistical intervals using Around:

Specific Values  (4)

Limiting value at infinity:

The first three zeros:

Find the first zero of AiryBi using Solve:

AiryBiZero threads elementwise over lists:

Visualization  (2)

Display zeros of AiryBi function:

Show the first zero less than :

Series Expansion  (1)

Asymptotic behavior of AiryBiZero[k] for large k:

Applications  (1)

Display zeros on the plot:

Wolfram Research (2007), AiryBiZero, Wolfram Language function, https://reference.wolfram.com/language/ref/AiryBiZero.html.

Text

Wolfram Research (2007), AiryBiZero, Wolfram Language function, https://reference.wolfram.com/language/ref/AiryBiZero.html.

CMS

Wolfram Language. 2007. "AiryBiZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AiryBiZero.html.

APA

Wolfram Language. (2007). AiryBiZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AiryBiZero.html

BibTeX

@misc{reference.wolfram_2024_airybizero, author="Wolfram Research", title="{AiryBiZero}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/AiryBiZero.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_airybizero, organization={Wolfram Research}, title={AiryBiZero}, year={2007}, url={https://reference.wolfram.com/language/ref/AiryBiZero.html}, note=[Accessed: 18-November-2024 ]}