AlgebraicNumberPolynomial[a,x]
AlgebraicNumberオブジェクト a に対応する x における多項式を返す.


AlgebraicNumberPolynomial
AlgebraicNumberPolynomial[a,x]
AlgebraicNumberオブジェクト a に対応する x における多項式を返す.
詳細
- AlgebraicNumber[θ,{c0,c1,…}]の形の代数的数 a について,AlgebraicNumberPolynomial[a,x]は,x を θ で置換することによって a が得られる多項式
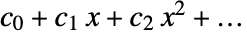 である.
である.
例題
すべて開く すべて閉じる例 (1)
スコープ (3)
特性と関係 (1)
AlgebraicNumberは定義により代数的数の多項式関数である:
考えられる問題 (1)
入力はAlgebraicNumberオブジェクトか有理数でなければならない:
関連するガイド
-
▪
- 代数的整数論
テキスト
Wolfram Research (2007), AlgebraicNumberPolynomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html.
CMS
Wolfram Language. 2007. "AlgebraicNumberPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html.
APA
Wolfram Language. (2007). AlgebraicNumberPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html
BibTeX
@misc{reference.wolfram_2025_algebraicnumberpolynomial, author="Wolfram Research", title="{AlgebraicNumberPolynomial}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_algebraicnumberpolynomial, organization={Wolfram Research}, title={AlgebraicNumberPolynomial}, year={2007}, url={https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html}, note=[Accessed: 05-February-2026]}