AlgebraicNumberPolynomial
AlgebraicNumberPolynomial[a,x]
给出与 AlgebraicNumber 对象 a 相应的关于 x 的多项式.
更多信息
- 对于形如 AlgebraicNumber[θ,{c0,c1,…}] 的代数数 a 而言,AlgebraicNumberPolynomial[a,x] 为多项式
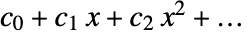 ,将 θ 代入其中的 x 可以得到 a.
,将 θ 代入其中的 x 可以得到 a.
范例
打开所有单元关闭所有单元基本范例 (1)
范围 (3)
属性和关系 (1)
AlgebraicNumber 定义为一个代数数的多项式函数:
可能存在的问题 (1)
该输入必须是一个 AlgebraicNumber 对象或者是一个有理数:
Wolfram Research (2007),AlgebraicNumberPolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html.
文本
Wolfram Research (2007),AlgebraicNumberPolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html.
CMS
Wolfram 语言. 2007. "AlgebraicNumberPolynomial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html.
APA
Wolfram 语言. (2007). AlgebraicNumberPolynomial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AlgebraicNumberPolynomial.html 年