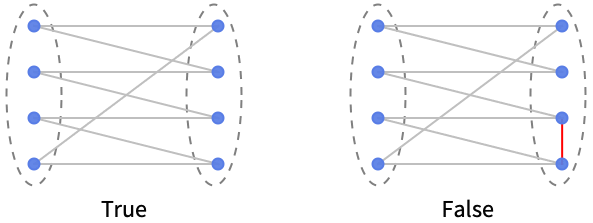
BipartiteGraphQ

BipartiteGraphQ[g]

グラフ g が二部グラフであればTrueを，そうでなければFalseを返す．

詳細

  • あるグラフの頂点が2つのグループに分けられ，すべての辺が両グループ間にあるとき，そのグラフは二部グラフである．

予備知識

  • BipartiteGraphQは，指定されたグラフが二部グラフかどうかを調べる．頂点集合が 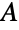と 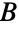の2つの独立集合（「部集合」と呼ばれる）に分割できるグラフは二部グラフである．独立頂点集合は，同じ辺に接続する頂点は存在しないという条件を満たす頂点集合である．換言すれば，二部グラフの辺の片方の端点はすべて 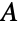に含まれ，もう片方の端点はすべて 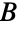に含まれる．BipartiteGraphQは，あるグラフが二部グラフのときはTrue を返し，それ以外のときはFalseを返す．グラフが二部グラフになる条件と同等の条件に，奇数長の閉路がない，彩色数が最大2である，等がある．木（および森）は閉路を含まない．したがって自動的に二部グラフである．二部グラフの族には，奇数個の頂点を持つ閉路グラフ，格子グラフ，超立方体グラフ，ナイト（騎士）グラフ，スターグラフ（木であるため二部グラフである）等が含まれる．
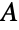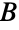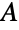  • 二部グラフは ある種の割り当て問題から自然発生した．例えば，労働者の集合 と常勤の仕事の集合 は， と 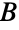の部集合があり労働者が仕事を行う資格がある場合に労働者とその仕事を繋ぐ辺がある二部グラフを構築する．雇用が最大になるように労働者を仕事に割り当てることは，最大独立辺集合を求めることに等しい．
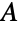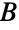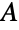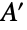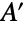  • グラフ理論における多くの基本的な結果が二部グラフを含んでいる．ケーニヒ(König)の線彩色定理は，二部グラフの線彩色数はグラフの最大次数と等しいと述べている．ケーニヒ・エゲルヴァーリ(König–Egerváry)の定理は，二部グラフのおける独立辺集合の最大サイズは頂点被覆の最小サイズに等しいと述べている．オーレ(Ore)の欠損公式は，グラフに部集合 と があるなら，共通する値は， のすべての部分集合 上で最大の から 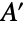内のある点に接続する 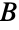の頂点数を引いたものを 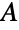のサイズから引いたものであると述べている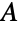． のどの部分集合も 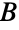における近傍より多くの頂点を含まない特殊ケースの場合，オーレの欠損公式はホール(Hall)の結婚定理となる．この定理は，この条件が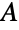， の各頂点に接続する辺の独立集合の存在に等しいと述べている．
  • CompleteGraph[{m,n}]は，部集合 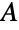と 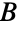についての，サイズがそれぞれ m と n の完全二部グラフを返す．この二部グラフは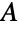， のすべての頂点が 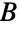の各頂点に接続している二部グラフである．

例題

すべて開くすべて閉じる

例  (2)

グラフが二部グラフかどうか調べる：

すべてのグラフが二部グラフである訳ではない：

スコープ  (6)

BipartiteGraphQは無向グラフに使うことができる：

有向グラフに使う：

多重グラフに：

混合グラフに：

BipartiteGraphQはグラフではない式に対してはFalseを返す：

BipartiteGraphQは大きいグラフに使うことができる：

特性と関係  (8)

二部グラフには自己ループがない：

木はどれも二部グラフである：

別々の始まりと終りの頂点を持つPathGraphは二部グラフである：

面がすべて偶数本の辺からなる任意の平面グラフは二部グラフである：

偶数の頂点があるCycleGraphは二部グラフである：

CompleteGraph は二部グラフである：

TuranGraph は二部グラフである：

奇数のサイクルがない限りかつそのときに限りグラフは二部グラフである：

Wolfram Research (2010), BipartiteGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.

テキスト

Wolfram Research (2010), BipartiteGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.

CMS

Wolfram Language. 2010. "BipartiteGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.

APA

Wolfram Language. (2010). BipartiteGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BipartiteGraphQ.html

BibTeX

@misc{reference.wolfram_2024_bipartitegraphq, author="Wolfram Research", title="{BipartiteGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/BipartiteGraphQ.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bipartitegraphq, organization={Wolfram Research}, title={BipartiteGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/BipartiteGraphQ.html}, note=[Accessed: 18-November-2024 ]}