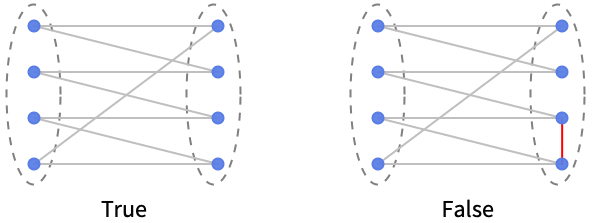
BipartiteGraphQ
背景
- BipartiteGraphQ 检验指定的图是否为二分图. 如果一个图的顶点能够被分成两个不相交的独立集合(称作"分裂集合")
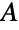 和
和 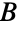 ,其中独立集合内的任意两个顶点均没有共同边,则该图为二分图. 也就是说,二分图的所有边在
,其中独立集合内的任意两个顶点均没有共同边,则该图为二分图. 也就是说,二分图的所有边在  和
和 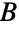 内各有一个端点. 如果图为二分图,BipartiteGraphQ 返回 True,否则返回 False.
图为二分图的等价条件包括缺少奇数长度的环和色数最多为两个. 树(和森林)不含有环,因此自然是二分的. 二分图的家族包括顶点数为偶数的环图、网格图、超立方体图、骑士图和星形图(由于是树图自然为二分图).
内各有一个端点. 如果图为二分图,BipartiteGraphQ 返回 True,否则返回 False.
图为二分图的等价条件包括缺少奇数长度的环和色数最多为两个. 树(和森林)不含有环,因此自然是二分的. 二分图的家族包括顶点数为偶数的环图、网格图、超立方体图、骑士图和星形图(由于是树图自然为二分图). - 二分图是在模拟某些任务分配问题时自然产生的. 例如,已知工人的集合为
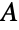 ,全时工作的集合为
,全时工作的集合为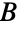 ,构造一个由分裂集合
,构造一个由分裂集合 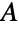 和
和 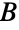 组成的二分图,如果一个工人能胜任某项工作,则用边将工人和工作连接. 求使得工人利用最大化的任务分配方式等价于求最大的独立边集合.
组成的二分图,如果一个工人能胜任某项工作,则用边将工人和工作连接. 求使得工人利用最大化的任务分配方式等价于求最大的独立边集合. - 图论中的许多基础性结果涉及二分图. 根据 König 线染色定理,二分图的边色数等于它们的最大度数. König–Egerváry 定理表明,对于二分图,独立边集合的最大尺寸等于顶点覆盖的最小尺寸. Ore 缺陷公式指出,如果一个图有分裂集合
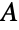 和
和 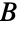 ,则该公共值等于
,则该公共值等于 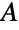 的大小减去
的大小减去 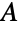 的所有子集
的所有子集 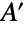 ,和
,和 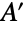 的大小减去
的大小减去 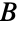 中与
中与 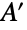 中顶点相邻的顶点数的最大值. 在特殊情况下,
中顶点相邻的顶点数的最大值. 在特殊情况下,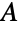 的子集的顶点数全部小于
的子集的顶点数全部小于 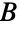 中它的近邻数,Ore 缺陷公式则成为 Hall 结婚定理,后者指出,这个条件等价于入射到
中它的近邻数,Ore 缺陷公式则成为 Hall 结婚定理,后者指出,这个条件等价于入射到 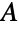 的各顶点的一组独立的边集合的存在性.
的各顶点的一组独立的边集合的存在性. - CompleteGraph[{m,n}] 返回在分裂集合
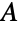 和
和 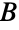 上尺寸分别为 m 和 n 的完全二分图,它在
上尺寸分别为 m 和 n 的完全二分图,它在 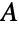 中的每个顶点都与
中的每个顶点都与 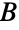 中的每个顶点相连.
中的每个顶点相连.
范例
打开所有单元关闭所有单元范围 (6)
属性和关系 (8)
含有不同的起始顶点和末端顶点的 PathGraph 是二部图:
一个顶点数为偶数的 CycleGraph 是二部图:
一个 CompleteGraph ![]() 是二部图:
是二部图:
一个 TuranGraph ![]() 是二部图:
是二部图:
Wolfram Research (2010),BipartiteGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
文本
Wolfram Research (2010),BipartiteGraphQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
CMS
Wolfram 语言. 2010. "BipartiteGraphQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
APA
Wolfram 语言. (2010). BipartiteGraphQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BipartiteGraphQ.html 年