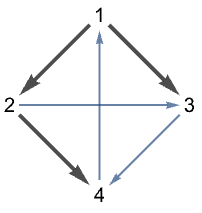
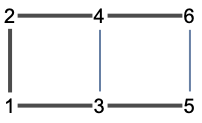
BreadthFirstScan[g,s,{"event1"f1,"event2"f2,…}]
执行图 g 的广度优先搜索,以顶点 s 为起始点,每次出现 "eventi" 时计算 fi.
BreadthFirstScan[g,{"event1"f1,"event2"f2,…}]
执行整个图 g 的广度优先搜索.
BreadthFirstScan[{vw,…},…]
使用 vw 规则来指定图 g.




BreadthFirstScan
BreadthFirstScan[g,s,{"event1"f1,"event2"f2,…}]
执行图 g 的广度优先搜索,以顶点 s 为起始点,每次出现 "eventi" 时计算 fi.
BreadthFirstScan[g,{"event1"f1,"event2"f2,…}]
执行整个图 g 的广度优先搜索.
BreadthFirstScan[{vw,…},…]
使用 vw 规则来指定图 g.
更多信息



- BreadthFirstScan 广度优先扫描也称为广度优先搜索(BFS)或广度优先遍历.
- BreadthFirstScan[g,s,{…}] 以广度优先顺序访问图 g 中与顶点 s 相连接的顶点.
- 广度优先搜索首先访问与当前被访问的顶点相邻接的所有顶点.
- BreadthFirstScan[g,{…}] 在 g 的顶点列表中从第一个顶点开始执行多个广度优先搜索,然后从顶点列表中第一个未被访问的顶点开始,搜索每个连接的分量.
- BreadthFirstScan[g,…] 给出表示一棵树的 {w1,w2,…} 的列表,其中 wi 是 vi 的前趋结点,而{v1,v2,…} 是 g 的顶点列表.
- 提供对顶点的探索的事件包括:
-
"DiscoverVertex" 当找到顶点时 "UnvisitedVertex" 当未访问顶点被再次找到时 "VisitedVertex" 当已访问顶点被再次找到时 - 当顶点 u 从已访问顶点 v 被发现,并且 v 距离起始顶点 s 的距离为 d 时,"DiscoverVertex"->fd 调用 fd[u,v,d].
- 当未访问顶点 u 从已访问顶点 v 中再次找到时,"UnvisitedVertex"->fru 调用 fru[u,v].
- 当已访问顶点 u 从已访问顶点 v 中再次找到时,"VisitedVertex"->frv 调用 frv[u,v].
- 提供对顶点的访问的选项包括:
-
"PrevisitVertex" 在访问一个顶点之前 "PostvisitVertex" 在访问一个顶点之后 - 在顶点 u 被访问之前,"PrevisitVertex"->fs 调用 fs[u].
- 在顶点 u 被访问之后,"PostvisitVertex"->fe 调用 fe[u].
- 一棵广度优先树是由在广度优先搜索中所遍历的边生成的树.
- 提供对从已访问顶点开始的边的搜索的选项包括:
-
"FrontierEdge" 在广度优先搜索树中的边 "CycleEdge" 不在广度优先搜索树中的边 - 对于边 vu,"FrontierEdge"->ffe 调用 ffe[vu],其中顶点 v 正在被访问,u 还未被访问过. 通常对扫描广度优先搜索树是很有用的.
- 对于边 vu,"CycleEdge"->fce 调用 fce[vu],其中顶点 v 正在被访问,u 已经被访问过. 通常对寻找不位于广度优先搜索树中的环或者边是很有用的.
- 对于一个无向图,用于 callback 的边是无向边 vu.
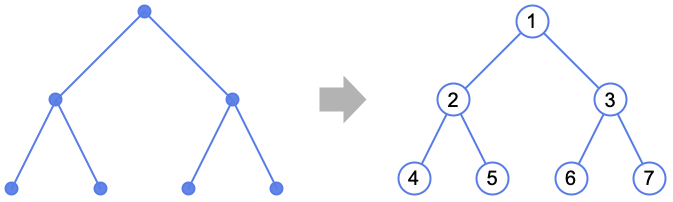
范例
打开所有单元 关闭所有单元范围 (18)
基本用途 (6)
顶点查找过程 (3)
搜索树的前趋结点 (5)
BreadthFirstScan 返回广度优先搜索树中前趋结点的列表:
当搜索产生一棵生成树时,TreeGraph 更加便捷:
前趋结点也可以通过 "DiscoverVertex" 事件得到:
使用 VertexList 初始化,并且当找到一个顶点时,重新赋值:
与 BreadthFirstScan 返回的值相比较:
选项 (42)
"CycleEdge" (8)
在 "OutEdges" 之后,每条边或者传递给 "FrontierEdge" 或者传递给 "CycleEdge":
当且仅当一条边产生第一次搜索的顶点时,触发 "FrontierEdge":
在 "CycleEdge" 之后,触发 "VisitedVertex" 或者 "UnvisitedVertex":
当且仅当相邻的顶点已经被访问时,触发 "VisitedVertex":
在一棵有向树中,标明对 "CycleEdge" 函数的调用:
在一个有向 CycleGraph 中:
在一个无向 CycleGraph 中:
"DiscoverVertex" (8)
在 "FrontierEdge" 之后,对相邻的顶点触发 "DiscoverVertex":
当一个顶点第一次被搜索时,触发 "DiscoverVertex" 事件:
"DiscoverVertex" 事件在对 "PrevisitVertex" 进行调用之前触发:
在一棵有向树中,显示传递给 "DiscoverVertex" 函数的变量:
在一个有向 CycleGraph 中:
在一个无向 CycleGraph 中:
"FrontierEdge" (8)
在 "OutEdges" 后,每条边或者传递给 "FrontierEdge" 或者传递给 "CycleEdge":
当且仅当一条边产生的顶点第一次被搜索才触发 "FrontierEdge":
在 "FrontierEdge" 之后,对相邻顶点触发 "DiscoverVertex":
对一棵有向树中的每条边调用 "FrontierEdge" 函数:
突出显示一个有向 CycleGraph 中的广度优先搜索树:
在一个无向 CycleGraph 中:
"PostvisitVertex" (2)
"PrevisitVertex" (2)
"UnvisitedVertex" (7)
在 "CycleEdge" 后,或者触发 "VisitedVertex" 或者触发 "UnvisitedVertex":
当且仅当相邻的顶点还未被访问时,触发 "UnvisitedVertex":
在一棵有向树中标明传递给 "UnvisitedVertex" 函数的前趋:
在有向的 CycleGraph 中:
在无向的 CycleGraph 中:
"VisitedVertex" (7)
在 "CycleEdge" 后,触发 "VisitedVertex" 或者 "UnvisitedVertex":
当且仅当相邻的顶点已经被访问才触发 "VisitedVertex":
在一棵有向树中标明传递给 "VisitedVertex" 函数的前趋结点:
在一个有向 CycleGraph 中:
在一个无向 CycleGraph 中:
应用 (17)
基本应用 (10)
显示搜索过程 (4)
利用 "FrontierEdge" 构建一个广度优先搜索树:
在一个有向图中,"CycleEdge" 边可以归类为后边(back edges)或者交叉边(cross edges):
在每个顶点的时间轴中,在搜索的时间处放置一个点,从 previsit 到 postvisit 处放置一条线:
在一个有向 CycleGraph:
在一个无向 CycleGraph 中:
把搜索过的顶点变为红色,活动中的顶点变为黄色,访问过的顶点变为蓝色,将不是树的边颜色用来显示它们是否产生 "UnvisitedVertex" (红色)或者 "VisitedVertex" (蓝色)调用:
最短路径应用 (3)
与 FindShortestPath 相比较:
在一个空手道俱乐部中,Zachary 的传统友谊网络的中介中心性:
在考虑从每个顶点的所有最短路径时,对 "BetweennessCentrality" 进行累积:
文本
Wolfram Research (2010),BreadthFirstScan,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BreadthFirstScan.html (更新于 2015 年).
CMS
Wolfram 语言. 2010. "BreadthFirstScan." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/BreadthFirstScan.html.
APA
Wolfram 语言. (2010). BreadthFirstScan. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BreadthFirstScan.html 年
BibTeX
@misc{reference.wolfram_2025_breadthfirstscan, author="Wolfram Research", title="{BreadthFirstScan}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BreadthFirstScan.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_breadthfirstscan, organization={Wolfram Research}, title={BreadthFirstScan}, year={2015}, url={https://reference.wolfram.com/language/ref/BreadthFirstScan.html}, note=[Accessed: 05-March-2026]}