ClebschGordan

ClebschGordan[{j1,m1},{j2,m2},{j,m}]

からへの分解に対する，クレプシュ・ゴルダン(Clebsch–Gordan)係数を与える

詳細

  • クレプシュ・ゴルダン係数は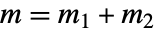，と三角不等式を満足させる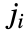を除いて削除される．
  • ClebschGordanのパラメータとして，整数，2分の1の倍数，そしてシンボルが使われる．
  • Wolfram言語では，クレプシュ・ゴルダン係数の位相には，エドモンド法表記が使われる．
  • Wolfram言語のクレプシュ・ゴルダン係数と3‐ 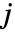シンボルは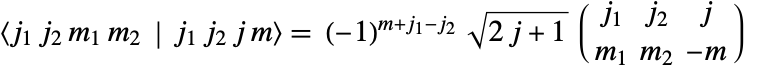の関係を満足する．

例題

すべて開くすべて閉じる

例  (2)

クレプシュ・ゴルダン係数を整数引数で評価する：

記号引数を使って厳密な記号的答を得る：

スコープ  (2)

ClebschGordanは整数と半整数の引数を取ることができる：

記号入力についてClebschGordanを評価するとThreeJSymbolになる：

アプリケーション  (3)

クレプシュ・ゴルダン係数を と の関数としてプロットする：

球面調和関数を2つの球面調和関数の積の和に分解する：

角運動量演算子を球面調和関数に適用する：

特性と関係  (2)

ClebschGordanの完全に記号的な場合を評価する：

和の直交性を分解する：

考えられる問題  (1)

の場合には，メッセージが出力され，0という結果が返される：

おもしろい例題  (1)

クレプシュ・ゴルダン係数によって形成された等高線を可視化する：

Wolfram Research (1991), ClebschGordan, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClebschGordan.html.

テキスト

Wolfram Research (1991), ClebschGordan, Wolfram言語関数， https://reference.wolfram.com/language/ref/ClebschGordan.html.

CMS

Wolfram Language. 1991. "ClebschGordan." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ClebschGordan.html.

APA

Wolfram Language. (1991). ClebschGordan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ClebschGordan.html

BibTeX

@misc{reference.wolfram_2025_clebschgordan, author="Wolfram Research", title="{ClebschGordan}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/ClebschGordan.html}", note=[Accessed: 06-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_clebschgordan, organization={Wolfram Research}, title={ClebschGordan}, year={1991}, url={https://reference.wolfram.com/language/ref/ClebschGordan.html}, note=[Accessed: 06-March-2025 ]}