ClebschGordan

ClebschGordan[{j1,m1},{j2,m2},{j,m}]

给出以 的形式分解 所得的克莱布什－高登系数.

更多信息

  • Clebsch–Gordan系数只有在 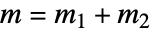和 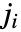满足三角不等式时不等于零.
  • ClebschGordan 的参数可以是整数、半整数或符号表达式.
  • Wolfram 语言对于克莱布什－高登系数的相位使用标准的 Edmonds 规范.
  • Wolfram 语言中的克莱布什－高登系数和 3‐ 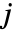符号满足以下关系式 .

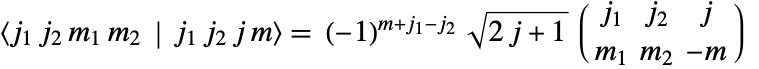范例

打开所有单元关闭所有单元

基本范例  (2)

用整数参数计算克莱布什－高登系数：

利用符号自变量得到确切的符号答案：

范围  (2)

ClebschGordan 可用于整数和半整数：

对于符号输入，ClebschGordan 的计算结果用 ThreeJSymbol 表示：

应用  (3)

描绘作为 和 的函数的 Clebsch–Gordan 系数：

把一个球谐函数分解成为两个球谐函数的乘积之和：

将角动量算子应用到球谐函数中：

属性和关系  (2)

计算 ClebschGordan 的全符号情况：

论证 ‐和数正交性：

可能存在的问题  (1)

当 时，生成一则信息，并返回结果 0 ：

巧妙范例  (1)

可视化由克莱布什－高登系数构建的等高线：

Wolfram Research (1991)，ClebschGordan，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClebschGordan.html.

文本

Wolfram Research (1991)，ClebschGordan，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ClebschGordan.html.

CMS

Wolfram 语言. 1991. "ClebschGordan." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ClebschGordan.html.

APA

Wolfram 语言. (1991). ClebschGordan. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ClebschGordan.html 年

BibTeX

@misc{reference.wolfram_2024_clebschgordan, author="Wolfram Research", title="{ClebschGordan}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/ClebschGordan.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_clebschgordan, organization={Wolfram Research}, title={ClebschGordan}, year={1991}, url={https://reference.wolfram.com/language/ref/ClebschGordan.html}, note=[Accessed: 18-November-2024 ]}