ControllabilityGramian

ControllabilityGramian[ssm]

gives the controllability Gramian of the state-space model ssm.

Details and Options

  • The state-space model ssm can be given as StateSpaceModel[{a,b,…}], where a and b represent the state and input matrices in either the continuous-time system or the discrete-time system:
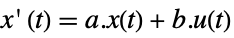
  • continuous-time system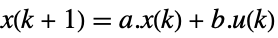
    discrete-time system
  • The controllability Gramian:
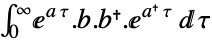
  • continuous-time system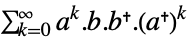
    discrete-time system
  • For asymptotically stable systems, the Gramian 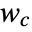can be computed as the solution of a Lyapunov equation:
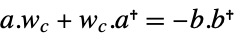
  • continuous-time system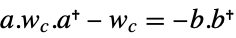
    discrete-time system
  • For a StateSpaceModel with a descriptor matrix, ControllabilityGramian returns a pair of matrices {wcs,wcf}, where wcs is associated with the slow subsystem, and wcf is associated with the fast subsystem.
  • The controllability Gramians only exist for descriptor systems in which Det[λ e-a]≠0 for some λ.

Examples

open allclose all

Basic Examples  (1)

The controllability Gramian of a state-space model:

Scope  (4)

The controllability Gramian of a continuous-time system:

The controllability Gramian of a discrete-time system:

The controllability Gramian of a symbolic system:

The controllability Gramian of a descriptor system:

Applications  (1)

Check if a system is controllable:

Properties & Relations  (7)

The controllability Gramian has the dimension of the state matrix:

If the controllability Gramian has full rank, the system is controllable:

The controllability Gramian of a controllable and asymptotically stable system is symmetric and positive definite:

The controllability Gramians of asymptotically stable systems satisfy the corresponding Lyapunov equations:

The controllability Gramian is the observability Gramian of the dual system:

A descriptor state-space model gives two Gramians:

The systems is completely controllable if and only if the sum is positive definite:

The fast and slow subsystem Gramians are computed from the Kronecker decomposition:

Split the decoupled states:

The slow subsystem yields a Gramian for the slow states and a zero matrix:

The fast subsystem yields a Gramian for the fast states and a zero matrix:

Inversing the Kronecker transformation gives the Gramians for the original system:

This gives the same result as using ControllabilityGramian directly:

Possible Issues  (1)

The controllability Gramian is not defined for a system that is not asymptotically stable:

Wolfram Research (2010), ControllabilityGramian, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllabilityGramian.html (updated 2012).

Text

Wolfram Research (2010), ControllabilityGramian, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllabilityGramian.html (updated 2012).

CMS

Wolfram Language. 2010. "ControllabilityGramian." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/ControllabilityGramian.html.

APA

Wolfram Language. (2010). ControllabilityGramian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ControllabilityGramian.html

BibTeX

@misc{reference.wolfram_2024_controllabilitygramian, author="Wolfram Research", title="{ControllabilityGramian}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ControllabilityGramian.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_controllabilitygramian, organization={Wolfram Research}, title={ControllabilityGramian}, year={2012}, url={https://reference.wolfram.com/language/ref/ControllabilityGramian.html}, note=[Accessed: 18-November-2024 ]}