ControllabilityGramian

ControllabilityGramian[ssm]

给出状态空间模型 ssm 的可控性格拉姆矩阵.

更多信息和选项

  • 状态空间模型 ssm 可以以 StateSpaceModel[{a,b,…}] 形式给出，其中 a 和 b 表示连续或离散时间系统的状态和输入矩阵：
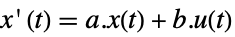
  • 连续时间系统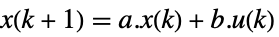
    离散时间系统
  • 可控性格拉姆矩阵：
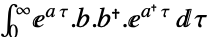
  • 连续时间系统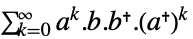
    离散时间系统
  • 对于渐近稳定系统，格拉姆 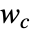可以计算为李雅普诺夫（Lyapunov）方程的解：
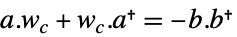
  • 连续时间系统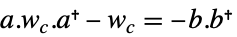
    离散时间系统
  • 对于具有描述符矩阵的 StateSpaceModel，ControllabilityGramian 返回一个矩阵对 {wcs,wcf}，其中 wcs 与慢速子系统相关联，而 wcf 与快速子系统相关联.
  • 只有当描述符系统对于某个 λ 有 Det[λ e-a]≠0 成立时，可控性格拉姆矩阵存在.

范例

打开所有单元关闭所有单元

基本范例  (1)

状态空间模型的可控性格拉姆矩阵：

范围  (4)

连续时间系统的可控性格拉姆矩阵：

离散时间系统的可控性格拉姆矩阵：

符号系统的可控性格拉姆矩阵：

描述符系统的可控性格拉姆矩阵:

应用  (1)

验证系统是否可控：

属性和关系  (7)

可控性格拉姆矩阵具有与状态矩阵相同的维数：

如果可控性格拉姆矩阵是满秩，则该系统是可控的：

一个可控的和渐近稳定系统的可控性格拉姆矩阵是对称的和正定的：

渐近稳定系统的可控性格拉姆矩阵满足相应的李雅普诺夫（Lyapunov）方程：

可控性格拉姆矩阵是对偶系统的可观测性格拉姆矩阵：

描述符状态空间模型给出两个格拉姆矩阵：

当且仅当总和是正定时，该系统是完全可控的：

快速与慢速子系统的格拉姆矩阵由克罗内克（Kronecker）分解计算得到：

对解耦状态进行拆分：

慢速子系统生成慢状态和零矩阵的格拉姆矩阵：

快速子系统生成快状态和零矩阵的格拉姆矩阵：

对克罗内克变换求逆，得到原系统的格拉姆矩阵：

这与直接使用 ControllabilityGramian 所得到的结果相同：

可能存在的问题  (1)

可控性格拉姆矩阵不是为非渐近稳定系统定义的：

Wolfram Research (2010)，ControllabilityGramian，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ControllabilityGramian.html （更新于 2012 年）.

文本

Wolfram Research (2010)，ControllabilityGramian，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ControllabilityGramian.html （更新于 2012 年）.

CMS

Wolfram 语言. 2010. "ControllabilityGramian." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2012. https://reference.wolfram.com/language/ref/ControllabilityGramian.html.

APA

Wolfram 语言. (2010). ControllabilityGramian. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ControllabilityGramian.html 年

BibTeX

@misc{reference.wolfram_2024_controllabilitygramian, author="Wolfram Research", title="{ControllabilityGramian}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ControllabilityGramian.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_controllabilitygramian, organization={Wolfram Research}, title={ControllabilityGramian}, year={2012}, url={https://reference.wolfram.com/language/ref/ControllabilityGramian.html}, note=[Accessed: 18-November-2024 ]}