Dilation

Dilation[image,ker]

構造化要素 ker についての image のモルフォロジー的な膨張処理を行う．

Dilation[image,r]

範囲 r の正方形についての膨張処理を行う

Dilation[data,…]

データ配列に膨張処理を行う．

詳細とオプション

  • Dilation派，ミンコフスキー(Minkowski)和としても知られている．
  • Dilationは，任意の3Dおよび2Dの画像（各チャンネルは別々に扱われる．）および任意の階数のデータ配列に使うことができる．
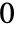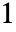  • 構造化要素 ker はとからなる行列である．
  • Dilation[image,r]はDilation[image,BoxMatrix[r]]と等価である．
  • 構造化要素が奇数次元になるように，自動的に0が加えられる． »
  • Dilationは画像の外側の画素に想定する値を指定するPaddingオプションを取る．
  • デフォルトで，画像にはPadding0が使われる．これは，すべてのチャンネルについて画素値0に等しい．

例題

すべて開くすべて閉じる

例  (3)

バイナリ画像の膨張処理：

グレースケール画像の膨張処理：

3Dの形の膨張処理：

スコープ  (13)

データ  (7)

2Dバイナリ配列の膨張処理：

バイナリ画像の膨張処理：

数値配列の膨張処理：

数値ベクトルの膨張処理：

グレースケール画像の膨張処理：

カラー画像の膨張処理：

データの記号配列の膨張処理：

パラメータ  (6)

水平の膨張：

垂直の膨張：

BoxMatrix[r]と等しい，半径 での膨張：

対角構造化要素による膨張：

偶数次元の構造化要素は右にゼロで充填される：

3Dカーネルを使った3D立体の膨張：

オプション  (2)

Padding  (2)

デフォルトで，配列に膨張処理を行う場合には，充填には可能な限り最小の数が使われる：

カスタムの充填を指定する：

デフォルトで，画像にはPadding->0が使われる：

カスタム充填を指定する：

アプリケーション  (2)

膨張処理を施すと，画像の白い部分が増え，小さく暗い特徴が取り除かれる：

外部的モルフォロジカル勾配を，膨張処理後の画像ともとの画像の差として計算する：

特性と関係  (2)

構造化要素が1を中心としているなら，バイナリ膨張は拡張的である：

拡張性は，f のすべての要素がDilation[f,ker]に含まれることを意味する：

ボックス構造化要素のある膨張処理はMaxFilterに等しい：

考えられる問題  (1)

すべてが0のカーネルを使った画像の膨張処理の結果はゼロイメージである：

すべてが0のカーネルを使った配列の膨張処理の結果は−∞の配列である：

Wolfram Research (2008), Dilation, Wolfram言語関数， https://reference.wolfram.com/language/ref/Dilation.html （2012年に更新）.

テキスト

Wolfram Research (2008), Dilation, Wolfram言語関数， https://reference.wolfram.com/language/ref/Dilation.html （2012年に更新）.

CMS

Wolfram Language. 2008. "Dilation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/Dilation.html.

APA

Wolfram Language. (2008). Dilation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Dilation.html

BibTeX

@misc{reference.wolfram_2024_dilation, author="Wolfram Research", title="{Dilation}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Dilation.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dilation, organization={Wolfram Research}, title={Dilation}, year={2012}, url={https://reference.wolfram.com/language/ref/Dilation.html}, note=[Accessed: 22-November-2024 ]}