Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

DualSystemsModel

DualSystemsModel[ssm]

给出状态空间模型 ssm 的对偶.

更多信息

状态空间模型 ssm 可以是一个标准或者描述器 StateSpaceModel.
标准 StateSpaceModel[{a,b,c,d}] 的原始和对偶系统：
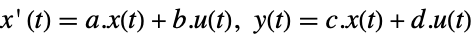
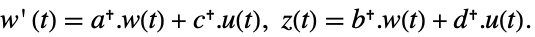
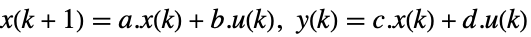
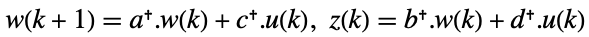
描述器 StateSpaceModel[{a,b,c,d,e}] 的原始和对偶系统：

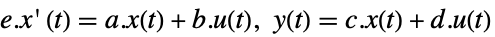
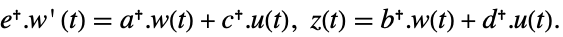
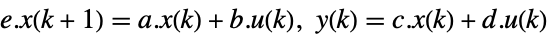
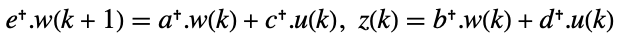
范例

打开所有单元关闭所有单元

基本范例 (1)

系统的对偶：

范围 (3)

对偶模型：

所有变量都被认为是复数：

简单地，假设所有变量都是实数：

只指定一些变量为实数：

描述器系统的对偶：

属性和关系 (4)

可控和可观测性实现具有对偶关系：

类似的关系存在于可控性伴型和可观测伴型之间：

一个不可控但可观测的模型：

对偶模型是可控的但不可观测：

系统的可控性矩阵是对偶系统的可观测性矩阵的共轭转置，反之亦然：

估计器增益是对偶模型的反馈增益的共轭转置，反之亦然：

顶部