EllipticExp

EllipticExp[u,{a,b}]

是与 EllipticLog 相反的. 它产生一个列表 {x,y} 以使得 u==EllipticLog[{x,y},{a,b}].

更多信息

  • 数学函数，同时适合符号和数值操作.
  • EllipticExp 给出与椭圆曲线 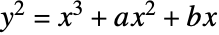相关的广义指数.
  • 对某些特定参数，EllipticExp 自动算出精确值.
  • EllipticExp 可求任意数值精度的值.

范例

打开所有单元关闭所有单元

基本范例  (2)

数值计算：

检查与反函数的关系：

绘制 EllipticExp 在数个实数周期内的分量：

范围  (10)

数值计算  (4)

数值化计算：

高精度计算：

输出的精度与输入的精度一致：

复数输入：

高精度的高效计算：

特殊值  (3)

在固定点的值：

符号式计算：

零处的值：

可视化  (2)

绘制各种参数值的 EllipticExp 函数：

绘制 EllipticExp[z,{1,2}] 实部：

绘制 EllipticExp[z,{1,2}] 虚部：

微分  (1)

关于 u 的一阶导：

当 a=10 且 b=1/3 时，绘制关于 u 的一阶导数：

应用  (4)

在椭圆曲线 上定义加法：

在椭圆曲线上利用加法增加一个有理数：

与 EllipticLog 进行比较：

在椭圆曲线上标出整数：

在复平面内可视化椭圆指数：

定义椭圆曲线 上的乘法：

在椭圆曲线上使用乘法来添加有理数：

乘积点的 EllipticLog 值等于相应因子的 EllipticLog 值之和：

属性和关系  (5)

求导：

由 EllipticExp[u,{a,b}] 返回的点 满足 ：

EllipticExp 与 WeierstrassP 函数及其导数有密切的关系：

比较数值：

计算椭圆指数及其导数：

EllipticExpPrime 可以用 EllipticExp 的分量来表示：

WeierstrassHalfPeriods 可以用来计算 EllipticExp 的两个线性独立周期：

比较 EllipticExp 在复平面内同位点的数值计算：

可能存在的问题  (1)

EllipticExp 是一个多值复变函数，所以不能总保持反比关系：

差异等于格的两个周期：

Wolfram Research (1988)，EllipticExp，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticExp.html.

文本

Wolfram Research (1988)，EllipticExp，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticExp.html.

CMS

Wolfram 语言. 1988. "EllipticExp." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticExp.html.

APA

Wolfram 语言. (1988). EllipticExp. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EllipticExp.html 年

BibTeX

@misc{reference.wolfram_2024_ellipticexp, author="Wolfram Research", title="{EllipticExp}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticExp.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ellipticexp, organization={Wolfram Research}, title={EllipticExp}, year={1988}, url={https://reference.wolfram.com/language/ref/EllipticExp.html}, note=[Accessed: 22-November-2024 ]}