WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

Wolfram言語＆システムドキュメントセンター

ExponentialMovingAverage

ExponentialMovingAverage

ExponentialMovingAverage[list,α]

平滑化定数が α の list の指数移動平均を返す．

詳細

平滑化定数 α は一般に0から1までの数であるが，任意の式でもよい．
ExponentialMovingAverage[x,α]は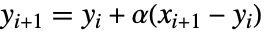，である結果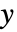のリストを生成する． »
ExponentialMovingAverage[list,α]の出力は，list と同じ長さである．
ExponentialMovingAverageは，数値データと記号データの両方を扱う．
ExponentialMovingAverageはSparseArrayオブジェクトおよびTemporalDataオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例 (2)

記号形式の指数移動平均：

数値の指数移動平均：

スコープ (4)

指数移動平均を機械精度で計算する：

行列の指数移動平均は行列である：

任意精度のリストの結果を求める：

任意精度で平滑係数の結果を求める：

一般化と拡張 (2)

SparseArrayについての結果を計算する：

TemporalDataオブジェクトについての結果を計算する：

アプリケーション (3)

ノイズのあるデータの平滑化：

初期値を使って指数移動平均を計算する：

金融時系列の指数移動平均を計算する：

特性と関係 (3)

指数移動平均の項は循環関係を満足する：

0の平滑化係数の指数移動平均は定数である：

1の平滑化係数の指数移動平均はもとのリストである：

Top