WOLFRAM

Wolfram Language & System Documentation Center

ExtendedGCD[n1,n2,…]

整数 niの拡張最大公約数を与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
特性と関係  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

ExtendedGCD

ExtendedGCD[n1,n2,…]

整数 niの拡張最大公約数を与える．

詳細

  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • ExtendedGCD[n1,n2,…]は，リスト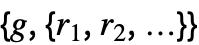{g,{r_(1),r_(2),...}}を返す．ただし，g はGCD[n1,n2,…]であり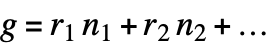，g=r_(1)n_(1)+r_(2)n_(2)+... であるものとする．
  • ExtendedGCDは自動的にリストに縫い込まれる．

例題

すべて開く すべて閉じる

例  (2)

2と3の拡張最大公約数：

いくつかの整数について拡張GCDを計算する：

スコープ  (1)

ExtendedGCDは要素単位でリストに適用される：

特性と関係  (1)

ExtendedGCDの最初の要素はGCDである：

おもしろい例題  (1)

Wolfram Research (1988), ExtendedGCD, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExtendedGCD.html （2003年に更新）.

テキスト

Wolfram Research (1988), ExtendedGCD, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExtendedGCD.html （2003年に更新）.

CMS

Wolfram Language. 1988. "ExtendedGCD." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2003. https://reference.wolfram.com/language/ref/ExtendedGCD.html.

APA

Wolfram Language. (1988). ExtendedGCD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExtendedGCD.html

BibTeX

@misc{reference.wolfram_2025_extendedgcd, author="Wolfram Research", title="{ExtendedGCD}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/ExtendedGCD.html}", note=[Accessed: 15-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_extendedgcd, organization={Wolfram Research}, title={ExtendedGCD}, year={2003}, url={https://reference.wolfram.com/language/ref/ExtendedGCD.html}, note=[Accessed: 15-September-2025]}