FactorialMomentGeneratingFunction
FactorialMomentGeneratingFunction[dist,t]
gives the factorial moment-generating function for the distribution dist as a function of the variable t.
FactorialMomentGeneratingFunction[dist,{t1,t2,…}]
gives the factorial moment-generating function for the multivariate distribution dist as a function of the variables t1, t2, ….
Details
- FactorialMomentGeneratingFunction is also known as probability generating function (pgf).
- FactorialMomentGeneratingFunction[dist,t] is equivalent to Expectation[tx,xdist].
- FactorialMomentGeneratingFunction[dist, {t1,t2,…}] is equivalent to Expectation[t1x1t2x2…,{x1,x2,…}dist].
- The i
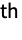 factorial moment can be extracted from a factorial moment-generating function fmgf through SeriesCoefficient[fmgf,{t,1,i}]i!.
factorial moment can be extracted from a factorial moment-generating function fmgf through SeriesCoefficient[fmgf,{t,1,i}]i!. - The probability for a discrete random variable to assume the value i can be extracted from a factorial moment-generating function expr through SeriesCoefficient[expr,{t,0,i}].
Examples
open allclose allBasic Examples (3)
Scope (5)
Applications (6)
Find the fmgf for the sum of ![]() i.i.d. geometric variates:
i.i.d. geometric variates:
Compare with the fmgf of NegativeBinomialDistribution:
Find the fmgf of the sum of a random number ![]() of i.i.d. geometric random variates, assuming
of i.i.d. geometric random variates, assuming ![]() follows PoissonDistribution:
follows PoissonDistribution:
Compare with the fmgf of PolyaAeppliDistribution:
Find the PDF of a non-negative integer random variate from its fmgf:
Use the probability generating function interpretation:
Show the probability mass function:
Construct a probability generating function for BernoulliDistribution:
Construct its Lagrange transformation, and use it as a new probability generating function:
Compare it with the probability generating function of a shifted GeometricDistribution:
Apply a Lagrange transformation to the probability generating function (pgf) of GeometricDistribution:
Reconstruct PDF:
The resulting distribution is known as Haight's distribution. It is only normalized to 1 for ![]() :
:
Show the probability mass function:
Find the distribution of the number of times a biased coin should be flipped until heads appear twice in a row. Let ![]() be the probability of heads. Event space is comprised of three types of events: tail (T), head then tail (HT), and two heads in a row (HH) with probabilities:
be the probability of heads. Event space is comprised of three types of events: tail (T), head then tail (HT), and two heads in a row (HH) with probabilities:
Find the fmgf of the random variate of interest, interpreting it as the total of the number of T events added to double the number of HT events plus 2:
Reconstruct PDF:
Properties & Relations (3)
FactorialMomentGeneratingFunction is equivalent to Expectation of ![]() :
:
For non-negative discrete variates, the fmgf is the probability generating function (pgf):
The factorial moments can be extracted from the factorial moment-generating function:
Alternatively, use SeriesCoefficient:
Possible Issues (2)
For some distributions with long tails, factorial moments of only several low orders are defined:
Correspondingly, the factorial moment-generating function is not defined:
FactorialMomentGeneratingFunction is not always known in closed form:
Text
Wolfram Research (2010), FactorialMomentGeneratingFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/FactorialMomentGeneratingFunction.html.
CMS
Wolfram Language. 2010. "FactorialMomentGeneratingFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FactorialMomentGeneratingFunction.html.
APA
Wolfram Language. (2010). FactorialMomentGeneratingFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FactorialMomentGeneratingFunction.html