FindHamiltonianPath
finds a Hamiltonian path in the graph g with the smallest total length.
FindHamiltonianPath[g,s,t]
finds a Hamiltonian path with the smallest total length from s to t.
Details and Options
- FindHamiltonianPath is also known as the Hamiltonian path problem.
- A Hamiltonian path visits each vertex exactly once.
- FindHamiltonianPath returns the list {} if no Hamiltonian path exists.
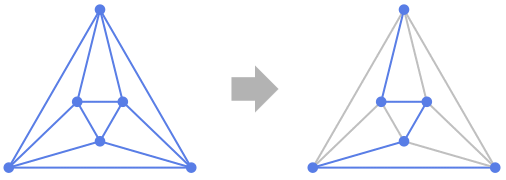
Examples
open allclose allBasic Examples (1)
Scope (3)
FindHamiltonianPath works with undirected graphs:
FindHamiltonianPath works with large graphs:
Options (1)
Applications (2)
Text
Wolfram Research (2015), FindHamiltonianPath, Wolfram Language function, https://reference.wolfram.com/language/ref/FindHamiltonianPath.html.
CMS
Wolfram Language. 2015. "FindHamiltonianPath." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindHamiltonianPath.html.
APA
Wolfram Language. (2015). FindHamiltonianPath. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindHamiltonianPath.html