FindTreeGameStrategies

FindTreeGameStrategies[tgame]

求 TreeGame tgame 的最优策略配置.

更多信息和选项

  • FindTreeGameStrategies 亦称为子博弈完美均衡 (SPE).
  • 树博弈策略配置是一组概率分布，指定任何玩家在任何给定动作节点的行为.
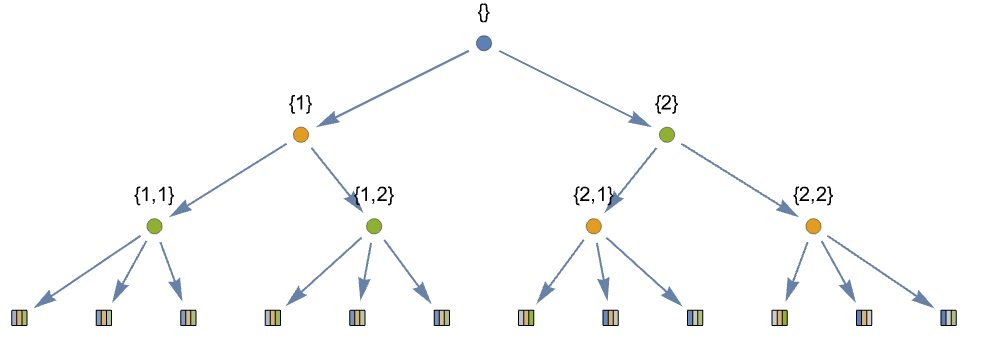
  • 要指定动作节点，请使用到达该动作节点所做出的选择列表，例如 {1} 表示采取第一个动作，{2,1} 表示先采取第二个动作，再采取第一个动作，{} 表示初始（根）动作节点.
  • 子博弈完美均衡被定义为一种树博弈策略，在这种状态下，没有玩家能够通过仅改变一个动作的概率分布来提高其收益.
  • 对于 TreeGame，FindTreeGameStrategies 将尝试为博弈中的所有玩家找到一组相互最优的策略.
  • 树博弈策略配置 <|…,playeri<|ni,1pri,1,…,ni,mipri,mi|>,…|> 指定 playeri 的动作节点 ni,j 中 playeri 的动作概率.
  • 例如，策略 <|"A" <|{} {0.7, 0.3}|>, "B" <|{2} {0.4, 0.6}|>|> <|"A" <|{} {0.7, 0.3}|>, "B" <|{2} {0.4, 0.6}|>|> 可以表示为：玩家“A”的第一个选择概率更高，而玩家“B”的第二个选择概率更高.

范例

打开所有单元关闭所有单元

基本范例  (4)

求树匹配硬币博弈（Tree Matching Pennies game）的最优策略：

求革命博弈（Revolution game）的最优策略：

可视化策略：

求升级博弈（Escalation game）的最优策略：

升级博弈的第一个动作基于概率，因此每个选择都会考虑策略：

生成 TreeGame：

找到所有子博弈完美均衡：

这更容易通过图表来直观展示：

范围  (3)

求市场进入博弈（Entry game）的最优策略：

考虑一个最后通牒博弈（Ultimatum game）：

求博弈的最优策略：

确定这对应于哪些动作：

求序贯形式的匹配硬币博弈的最优策略：

应用  (6)

社会学博弈  (2)

蜈蚣游戏（Centipede game）有两名玩家轮流做决定. 在每个回合，玩家可以选择“向下”结束游戏，也可以选择“向右”继续游戏（除了最后一个节点，在最后一个节点“向右”也会结束游戏）. 游戏时间越长，总收益越高. 提前结束游戏的玩家将获得更大的收益份额. 以下是该问题的一种表述：

求该博弈的最优策略：

从解的博弈树可以看出，在任何一步，博弈论最佳解决方案都是提前结束游戏：

配对硬币博弈的树状博弈版本是两个人各自选择正面或反面的博弈. 如果选择不同，则第 1 个人向第 2 个人支付 1 美元；如果选择相同，则第 2 个人向第 1 个人支付 1 美元. 生成配对硬币博弈的树状博弈版本：

求该博弈的最优博弈策略：

由于此博弈的序贯性质，第二个玩家占优势，可以根据第一个玩家的选择来选择最佳结果. 因此，无论第一个玩家选择什么均可以保证 {-1,1} 的收益：

休闲游戏  (2)

石头剪刀布是一个零和游戏，要么一个玩家赢，另一个玩家输，要么平局. 生成此游戏的树状博弈版本，其中第二个玩家可以根据第一个玩家的动作选择一个动作：

显然，在石头剪刀布的树状博弈情况下，第二个玩家总是可以选择最佳行动；因此第一个玩家先出手会处于劣势. 求最优博弈策略：

把井字游戏想象成一个三乘三的矩阵，其中 1 代表 "X"， 代表 "O"，0 代表空白：

考虑一个部分完成的井字游戏：

根据它构成 TreeGame：

可视化最优策略：

历史博弈  (2)

革命博弈（Revolution game）的定义如下. 殖民地可以选择叛乱或接受现状. 国家可以选择给予独立或镇压叛乱. 如果殖民地接受现状，国家可以选择对殖民地征税或不征税. 这种博弈通常在镇压叛乱的收益未知的情况下进行研究. 可视化这个博弈：

求解该博弈：

海军部署博弈是俾斯麦战役博弈的延伸，其中有一支军队逃跑，另一支军队追击：

求子博弈完美均衡：

巧妙范例  (1)

在彩虹战舰博弈中有两个玩家：石油公司（玩家 1）和环保主义者（玩家 2）. 石油公司拥有一个单一的石油开采平台，可在三个相邻的海域区域内移动. 每个区域每晚可非法开采的石油量不同. 环保人士需要抓到石油公司的非法开采行为才能获胜并结束游戏. 他们每天只能发射一个发射器，用于覆盖一个区域. 输入一个有三个单元格（左、中、右）的彩虹战舰游戏：

使用 TreeGamePlot 将博弈可视化：

忽略信息集，求该博弈的最优策略：

使用 TreeGamePlot 可以更轻松地将其可视化：

Wolfram Research (2025)，FindTreeGameStrategies，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

文本

Wolfram Research (2025)，FindTreeGameStrategies，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

CMS

Wolfram 语言. 2025. "FindTreeGameStrategies." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html.

APA

Wolfram 语言. (2025). FindTreeGameStrategies. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html 年

BibTeX

@misc{reference.wolfram_2025_findtreegamestrategies, author="Wolfram Research", title="{FindTreeGameStrategies}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html}", note=[Accessed: 06-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_findtreegamestrategies, organization={Wolfram Research}, title={FindTreeGameStrategies}, year={2025}, url={https://reference.wolfram.com/language/ref/FindTreeGameStrategies.html}, note=[Accessed: 06-July-2025 ]}