GraphHub

GraphHub[g]

g のもとになる単純グラフで頂点次数が最大である頂点集合を与える．

GraphHub[g,"In"]

最大頂点入次数の頂点集合を与える．

GraphHub[g,"Out"]

最大頂点出次数の頂点集合を与える．

GraphHub[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細

  • 頂点 v の頂点次数は v に接続している辺の本数である．
  • 有向グラフの場合，入次数は入ってくる辺の数，出次数は出ていく辺の数である，
  • 無向グラフの場合，辺は入辺と出辺の両方であるとみなされる．
  • GraphHubは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

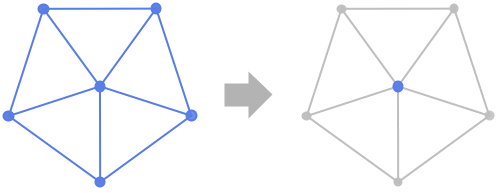
例題

すべて開くすべて閉じる

例  (1)

グラフのハブを求める：

ハイライトする：

スコープ  (5)

GraphHubは無向グラフに使うことができる：

有向グラフに使う：

規則を使ってグラフを指定する：

頂点の入次数および出次数についてハブを計算する：

GraphHubは大きいグラフに使うことができる：

アプリケーション  (7)

管理者は空手クラブの会員間の友人ネットワークのハブである：

親族の集会に最も多くの家族が参加した人を求める：

引用ネットワークで最も多く引用される出版物を求める：

他の出版物への言及が最も多い出版物：

2011年9月11日の悲劇的な出来事に結び付くテトリストのネットワーク．陰謀の首謀者がネットワークのハブである：

メディチ家は，フィレンツェの名家間の婚姻によるネットワークのハブである：

メディチ家は最も有力な一家であり媒介中心性が最も高い：

ロンドンの地下鉄網で隣接駅数が最も多い駅を求める：

2011年11月に「MathGroup」のメーリングリストに送られた電子メールのネットワークで最も多くの返信が送られたメッセージを求める：

この月の最も興味深い件名：

最大数のメッセージを生成したメッセージを計算する：

特性と関係  (11)

GraphHubはDegreeCentralityについてのグラフの中心を与える：

入次数中心性について：

出次数中心性について：

単純グラフの場合，GraphHubはVertexDegreeについての中心を与える：

あるいはVertexInDegreeについての中心を与える：

あるいはVertexOutDegreeについての中心を与える：

自己ループは無視される：

CompleteGraphの場合は，すべての頂点がハブである：

PathGraphの場合は，端点を除くすべての頂点がハブである：

CycleGraphの場合はすべての頂点がハブである：

サイズ5以上のWheelGraphの場合は，車輪のハブがグラフのハブである：

GridGraphの場合は，格子の端以外にあるすべての頂点が ハブである：

CompleteKaryTreeの場合，葉と根以外のすべての頂点がハブである：

EccentricityCentralityについてのグラフの中心はGraphCenterで得ることができる：

最大VertexEccentricityを持つ頂点集合はGraphPeripheryで得ることができる：

グラフのBetweennessCentralityの中心：

ClosenessCentralityの中心：

EigenvectorCentralityの中心：

考えられる問題  (1)

自己ループは数として考慮されない：

VertexDegreeを使って自己ループを含んだ中心を求める：

Wolfram Research (2012), GraphHub, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphHub.html （2015年に更新）.

テキスト

Wolfram Research (2012), GraphHub, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphHub.html （2015年に更新）.

CMS

Wolfram Language. 2012. "GraphHub." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphHub.html.

APA

Wolfram Language. (2012). GraphHub. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphHub.html

BibTeX

@misc{reference.wolfram_2024_graphhub, author="Wolfram Research", title="{GraphHub}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphHub.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphhub, organization={Wolfram Research}, title={GraphHub}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphHub.html}, note=[Accessed: 22-November-2024 ]}