IncludeSingularSolutions

IncludeSingularSolutions

DSolveのオプションで，非線形常微分方程式に対して一般解とともに特異解も返すかどうかを指定する．

詳細

  • 特異解は，包絡解あるいは均衡解としても知られている．
  • 非線形微分方程式の場合は，一般解の任意の定数に有限な数値を割り当てることでは特異解は得られない．特異解は，一般解で表される曲線の族の包絡線を構築することで得ることができる．
  • 例えば，一階常微分方程式の一般解が方程式方程式 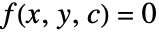（ここで 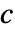は任意定数）によって与えられるなら，特異解は包絡線方程式 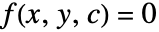と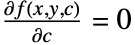を解くことで与えられる．
  • 以下の図は，一般解が直線の族である非線形常微分方程式の特異解（包絡線）を示している．
  • 特異解は，包絡線を構築することで説明できる光学におけるコースティクスや波面のような物理現象と密接な関係がある．
  • 次は，IncludeSingularSolutionsの可能な設定である．
  • False制約条件C[i]に従って一般解だけを返す
    True一般解と特異解の両方を返す

例題

すべて開くすべて閉じる

例  (2)

デフォルトで，DSolveは以下の常微分方程式の一般解を返す：

IncludeSingularSolutionsを使って一般解とともに特異解も計算する：

一般解を一般解の族によって形成された包絡線とともに可視化する：

ロジスティック方程式の一般解を求める：

この場合は特異解は「平衡」解の y=0 および y=1である：

一般解を平衡解とともに可視化する：

特性と関係  (1)

非線形常微分方程式の一般解を得る：

一般解で定義される曲線族についての包絡線を構築する：

IncludeSingularSolutionsを使って同じ結果を得る：

一般解を，その族によって形成された包絡線とともに可視化する：

Wolfram Research (2022), IncludeSingularSolutions, Wolfram言語関数， https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

テキスト

Wolfram Research (2022), IncludeSingularSolutions, Wolfram言語関数， https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

CMS

Wolfram Language. 2022. "IncludeSingularSolutions." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

APA

Wolfram Language. (2022). IncludeSingularSolutions. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html

BibTeX

@misc{reference.wolfram_2024_includesingularsolutions, author="Wolfram Research", title="{IncludeSingularSolutions}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_includesingularsolutions, organization={Wolfram Research}, title={IncludeSingularSolutions}, year={2022}, url={https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html}, note=[Accessed: 22-November-2024 ]}