WOLFRAM

Wolfram 语言与系统参考资料中心

IncludeSingularSolutions

是 DSolve 的一个选项，指定是否应将非线性常微分方程的奇异解与通解一起返回.

更多信息
Details and Options Details and Options
范例  
基本范例  
属性和关系  
参见
历史
按以下格式引用：

IncludeSingularSolutions

IncludeSingularSolutions

是 DSolve 的一个选项，指定是否应将非线性常微分方程的奇异解与通解一起返回.

更多信息

  • 奇异解也称为包络解或平衡解.
  • 奇异解不能通过将有限数值赋给非线性微分方程的通解中的任意常数来获得. 相反，它们可以通过构造由通解表示的曲线族的包络来获得.
  • 例如，如果一个一阶 ODE 的通解由 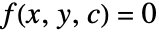给出，其中 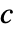为任意常数，则可通过求解包络方程 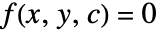和 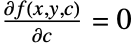获得奇异解.
  • 下图显示了非线性 ODE 的奇异解（包络），其通解是一个直线族.
  • 奇异解与物理现象密切相关，如光学中的焦散和波前等，可以使用包络结构来解释.
  • IncludeSingularSolutions 的可用设置为：
  • False只返回依赖于常数 C[i] 的通解
    True返回通解和奇异解

范例

打开所有单元 关闭所有单元

基本范例  (2)

默认情况下，DSolve 返回以下 ODE 的通解：

Wolfram Language code: DSolve[y'[x] ^ 2 - y'[x] * x + y[x] == 0, y[x], x]

用 IncludeSingularSolutions 计算通解和奇异解：

Wolfram Language code: DSolve[y'[x] ^ 2 - y'[x] * x + y[x] == 0, y[x], x, IncludeSingularSolutions -> True]

将通解与该族直线形成的包络一起可视化：

Wolfram Language code: Plot[Evaluate[{Table[x c - c^2, {c, -3, 3, 1 / 4}], x ^ 2 / 4}], {x, -3, 3}, PlotRange -> {-3, 3}]

求逻辑斯蒂方程的通解：

Wolfram Language code: DSolve[y'[x] == y[x] (1 - y[x]), y[x], x]

这种情况下，奇异解为“平衡”解 y=0 和 y=1：

Wolfram Language code: DSolve[y'[x] == y[x] (1 - y[x]), y[x], x, IncludeSingularSolutions -> True]

可视化通解及平衡解：

Wolfram Language code: Plot[{Table[(E^x/E^x + E^c), {c, -8, 8}], 1, 0}//Evaluate, {x, -12, 12}, PlotRange -> All]

属性和关系  (1)

获取非线性 ODE 的通解：

Wolfram Language code: DSolve[y[x] == x * y'[x] + y'[x] ^ 2 - 3y'[x], y[x], x]

构建由通解定义的曲线族的包络：

Wolfram Language code: sol = y[x] == (y[x] /. %[[1]])
Wolfram Language code: Eliminate[{sol, D[sol[[2]], C[1]] == 0}, C[1]]
Wolfram Language code: Solve[%, y[x]]

用 IncludeSingularSolutions 获取同样的结果：

Wolfram Language code: DSolve[y[x] == x * y'[x] + y'[x] ^ 2 - 3y'[x], y[x], x, IncludeSingularSolutions -> True]

可视化通解及由该曲线族形成的包络：

Wolfram Language code: Plot[Evaluate[{Table[-3 c + x c + c ^ 2, {c, -3, 3, 1 / 4}], (1/4) (-9 + 6 x - x^2)}], {x, -4, 7}, PlotRange -> {-3, 1}]
Wolfram Research (2022)，IncludeSingularSolutions，Wolfram 语言函数，https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

文本

Wolfram Research (2022)，IncludeSingularSolutions，Wolfram 语言函数，https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

CMS

Wolfram 语言. 2022. "IncludeSingularSolutions." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.

APA

Wolfram 语言. (2022). IncludeSingularSolutions. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html 年

BibTeX

@misc{reference.wolfram_2026_includesingularsolutions, author="Wolfram Research", title="{IncludeSingularSolutions}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html}", note=[Accessed: 12-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_includesingularsolutions, organization={Wolfram Research}, title={IncludeSingularSolutions}, year={2022}, url={https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html}, note=[Accessed: 12-July-2026]}