LatticeReduce

LatticeReduce[{v1,v2,…}]

整数ベクトル viの集合に対し，レンストラ(Lenstra)の格子算法による簡約された基底を与える．

詳細

  • viの要素は，整数，ガウスの整数，またはガウスの有理数を取り得る．

例題

すべて開くすべて閉じる

例  (1)

格子の簡約したノルム基底を返す：

アプリケーション  (3)

自明整数線形関係から始め，LatticeReduceはより興味深いものを作ることができる：

と についての の形の整数の線形関係を求める：

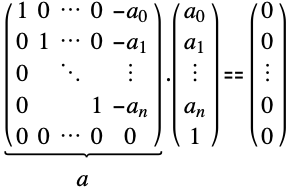
LatticeReduceは線形の関係を保存し，第3行は ，とを提供する：

について多項式関係 を求める：

自明な初期関係：

簡約された関係：

最初の関係：

線形関係 x0+x1 ArcTan[1]+x2 ArcTan[1/5]+x3 ArcTan[1/239]==0を求める：

初期の自明な関係：

簡約した関係：

最初の関係：

特性と関係  (2)

LatticeReduceは，同じ格子の新たな簡約した基底を生成する：

ノルムの積は減少する：

行列式，あるいは生成元の大きさは保存される：

格子は{v1,v2}で生成されるが，LatticeReduceで生成される{w1,w2}によっても生成される：

もとのセルはピンク，LatticeReduceによって生成されたものは青である：

考えられる問題  (1)

ベクトル集合は有理係数あるいはガウスの有理係数を持たなくてはならない：

Wolfram Research (1988), LatticeReduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/LatticeReduce.html.

テキスト

Wolfram Research (1988), LatticeReduce, Wolfram言語関数， https://reference.wolfram.com/language/ref/LatticeReduce.html.

CMS

Wolfram Language. 1988. "LatticeReduce." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LatticeReduce.html.

APA

Wolfram Language. (1988). LatticeReduce. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LatticeReduce.html

BibTeX

@misc{reference.wolfram_2024_latticereduce, author="Wolfram Research", title="{LatticeReduce}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/LatticeReduce.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_latticereduce, organization={Wolfram Research}, title={LatticeReduce}, year={1988}, url={https://reference.wolfram.com/language/ref/LatticeReduce.html}, note=[Accessed: 22-November-2024 ]}