Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

LatticeReduce

LatticeReduce[{v₁,v₂,…}]

给出向量 v_i 的集合的约化格基.

更多信息

v_i 的元素可以是整数、高斯整数或高斯有理数.

范例

打开所有单元关闭所有单元

基本范例 (1)

求一个格的约化基：

应用 (3)

从平凡的整数线性关系开始，LatticeReduce 可以产生更有趣的关系：

找出形如的整数线性关系，其中和：

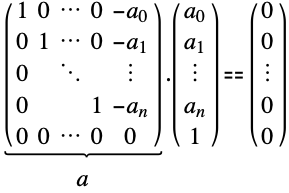
LatticeReduce 保留线性关系，并且第三行给出、和：

求时的多项式关系：

初始的平凡关系：

约化后的关系：

第一个关系：

找出线性关系 x₀+x₁ ArcTan[1]+x₂ ArcTan[1/5]+x₃ ArcTan[1/239]==0：

初始的平凡关系：

约化后的关系：

第一个关系：

属性和关系 (2)

LatticeReduce 对同一格产生一个新的约化基：

模的积将会减小：

但行列式、或生成单元的体积保持不变：

格是通过 {v₁,v₂} 生成的，同时也是通过 LatticeReduce 产生的 {w₁,w₂} 生成的：

原单元是粉红色的，LatticeReduce 产生的单元是蓝绿色的：

可能存在的问题 (1)

向量集必须是有理系数或高斯有理系数：

顶部