MatrixGame
MatrixGame[{{![]() ,…},…}]
,…},…}]
指定一个零和双人博弈,当玩家 1 和 2 分别采取动作 i 和 j 时,玩家 1 的收益为 ![]() ,玩家 2 的收益为 -
,玩家 2 的收益为 -![]() .
.
MatrixGame[{{{![]() ,
,![]() },…},…}]
},…},…}]
指定一个一般和双人博弈,当玩家 1 和 2 分别采取动作 i 和 j 时,玩家 1 的收益为 ![]() ,玩家 2 的收益为
,玩家 2 的收益为 ![]() .
.
MatrixGame[{…{{![]() ,…,
,…,![]() },…}…}]
},…}…}]
指定一个一般的 n 人博弈,当玩家 1 到 n 分别采取动作 i1,…,in 时,玩家 k 的收益为 ![]() .
.
更多信息和选项


- MatrixGame 也被称为标准型博弈(normal form game)、策略型博弈(strategic form game)、同步行动博弈(simultaneous move game)、双矩阵博弈(bimatrix game)和一次性博弈(one-shot game).
- MatrixGame 通常用于建模两个或更多玩家同时做出决策的问题. 具体例子包括石头剪刀布等手势游戏,以及囚徒困境和市场博弈等军事和商业博弈.
- 双人博弈可以用收益向量数组
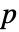 来描述. 如果玩家 1 有
来描述. 如果玩家 1 有 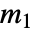 个可能的动作选择,玩家 2 有
个可能的动作选择,玩家 2 有 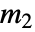 个可能的动作选择,则
个可能的动作选择,则 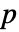 的维度是
的维度是 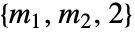 且 p〚i,j,k〛==
且 p〚i,j,k〛==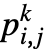 .
. 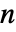 人博弈可以用深度为
人博弈可以用深度为 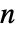 的收益向量数组
的收益向量数组 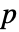 来描述. 如果玩家
来描述. 如果玩家 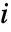 有
有 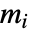 个可能的动作选择,则
个可能的动作选择,则 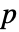 的维度是
的维度是 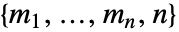 且 p〚i1,…,in,k〛==
且 p〚i1,…,in,k〛==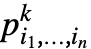 .
.- 最佳策略可使用 FindMatrixGameStrategies 得到. 策略的预期收益可使用 MatrixGamePayoff 得到.
- 可以提供以下选项:
-
GameActionLabels Automatic 用于动作的标签 GamePlayerLabels Automatic 用于玩家的标签 - MatrixGame 的属性包括以下属性,可以通过 g["prop"] 来访问:
-
"ComponentPayoffArray" 深度为 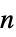 的
的 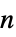 维玩家数组向量
维玩家数组向量 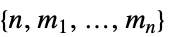
"Dataset" 收益的类型集 Dataset "GameActionLabels" list of action labels "GamePlayerLabels" list of player labels "PayoffArray" 由 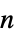 维收益向量组成的深度为
维收益向量组成的深度为 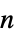 的数组
的数组 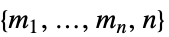
"Plot" 可视化 "TreeGame" 将矩阵博弈转换为树博弈 - There are two main forms to specify a matrix game, namely as an array of payoff vectors "PayoffArray" with dimensions
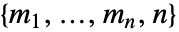 or as a vector of payoff arrays "ComponentPayoffArray" with dimensions
or as a vector of payoff arrays "ComponentPayoffArray" with dimensions 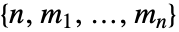 .
.

范例
打开所有单元关闭所有单元基本范例 (4)
范围 (10)
基本用法 (3)
分量和和复合数组 (2)
博弈属性 (1)
MatrixGame 对象包含提供有关博弈信息的属性:
"CompositePayoffArray" 属性给出游戏收益数组的复合形式:
"ComponentPayoffArray" 属性给出博弈收益数组的分量形式:
"PayoffArray" 属性也给出博弈收益数组的分量形式:
"PayoffData" 属性给出每个玩家可能获得的收益列表:
"Plot" 属性以与 MatrixGamePlot 相同的方式绘制矩阵博弈图:
"TreeGame" 属性将 MatrixGame 转换为 TreeGame:
选项 (4)
GameActionLabels (2)
这些名称可以通过 GameActionLabels 访问:
GamePlayerLabels (2)
应用 (11)
进化/生物博弈 (1)
普通的侧斑蜥蜴的雄性有三种不同的交配策略. 橙色颈雄蜥拥有大量的雌性“后宫”,蓝色颈雄蜥只守护一个或少数几个雌性并更具保护性,而黄色颈雄蜥则伪装是雌性并可以潜入雌性“后宫”. 根据实地观察,每种雄性策略的适应度都是已知的,这在很大程度上取决于已经存在的雄性策略的频率. ![]() 表示在第
表示在第 ![]() 种雄性策略占主导的环境中第
种雄性策略占主导的环境中第 ![]() 种策略的适应度:
种策略的适应度:
在混合种群中,每种策略的适应度可以通过交配博弈的预期收益来确定:
假设下一代每种策略的种群数量与当前种群数量成比例,且其适应度可得出以下进化动态:
休闲游戏 (3)
运动比赛 (1)
经济学博弈 (3)
三个饿汉去餐馆吃饭,决定平摊账单. 有便宜和昂贵的两种餐点可供选择. 便宜餐点的价格合理,为 10 美元,而昂贵餐点的合理价格应为 40 美元,但实际要价过高,为 50 美元. 将这种情况表示为 MatrixGame:
价格战是指这样一种博弈:多个企业都有兴趣提供最低价格,但每个企业的收益都与其选择的价格直接相关. 让我们考虑三家企业之间的价格战,其中每家企业都可以在低价和高价之间做出选择:
尽管各方的共同利益都在于尽可能提高价格,但竞争最终会在低价位形成纳什均衡:
一对夫妇可以从活动 A、B、C 中进行选择. 妻子喜欢 A,丈夫喜欢 B,他们都不喜欢 C. 使用 MatrixGame 来表示这种情况:
军事博弈 (1)
上校布洛托博弈(Colonel Blotto game)是一个双人零和博弈,玩家的任务是同时将有限的部队分配到多个战场上. 在每个战场上,部署最多部队的玩家获胜,最终收益等于获胜战场的总数. 让我们考虑一个有两个战场的上校布洛托博弈,其中布洛托上校有 2 个单位的部队,而敌人有 4 个单位的部队:
交通博弈 (2)
两个玩家同时开车到达一个十字路口. 每个玩家可以选择过马路或停下来. 如果两人都试图过马路,将导致致命事故. 成功过马路的收益为 1,而停下来的收益为 0. 将这种情况表示为 MatrixGame:
令人惊讶的是,当在道路网络中添加新的道路时,可能会导致整体交通状况变差,这被称为布雷斯悖论. 已知从 a 到 b 有两条不同的路径,一条经过 c,一条经过 d. 道路 ac 和 db 需要 20 n 分钟,其中 n 是道路上的驾驶员数量;cb 和 ad 需要 45 分钟,与驾驶员数量无关. 将道路网络表示为图:
按照上面的交通博弈,一般道路网络的建模和求解可以实现自动化. 这里的 start 和 end 是始顶点和终顶点,每个道路段的容量使用边权重进行编码:
在两条先前存在的路线之间切换的新可能性导致了类似囚徒困境的情形,其中唯一稳定的解导致与受限网络(65 分钟)相比更长的通勤时间(82 分钟):
可能存在的问题 (1)
如果给定的数组之一不是完整数组,MatrixGame 则不会进行运算:
文本
Wolfram Research (2025),MatrixGame,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MatrixGame.html.
CMS
Wolfram 语言. 2025. "MatrixGame." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGame.html.
APA
Wolfram 语言. (2025). MatrixGame. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixGame.html 年

