MatrixGamePayoff
MatrixGamePayoff[mgame,{s1,…,sn}]
行列ゲーム mgame について,戦略プロファイルが{s1,…,sn}である各プレーヤーの期待利得を与える.
MatrixGamePayoff[mgame,{s1,…,sn},"prop"]
各プレーヤーの利得特性"prop"を与える.
MatrixGamePayoff[mgame,"player1"s1,…,"playern"sn]
行列ゲーム mgame の名前付きの各プレーヤーの期待利得を連想を使った戦略プロファイル{s1,…,sn}で与える.
詳細

- MatrixGamePayoffは期待利得あるいは期待効用としても知られている.
- MatrixGamePayoffは,通常,各プレーヤーの戦略が与えられた場合のプレーヤーの期待利得の評価に使われる.
- 戦略プロファイル
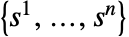 は,
は,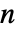 人のプレーヤーのための戦略のリストである.プレーヤー
人のプレーヤーのための戦略のリストである.プレーヤー 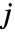 の戦略
の戦略 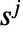 は異なる行動
は異なる行動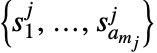 を取る確率のベクトルである.
を取る確率のベクトルである. - プレーヤー
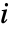 の期待利得は
の期待利得は 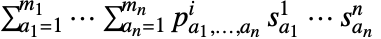 あるいは
あるいは 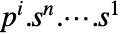 で与えられる.ここで,各記号は以下の通りである.
で与えられる.ここで,各記号は以下の通りである. -
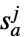
プレーヤー 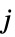 が行動
が行動 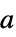 を取る確率
を取る確率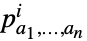
プレーヤー 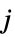 が行動
が行動 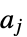 を取った場合のプレーヤー
を取った場合のプレーヤー 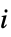 の利得
の利得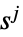
プレーヤー 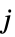 の戦略
の戦略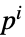
プレーヤー 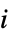 の利得配列
の利得配列 - 利得の特性"prop"には以下が含まれる.
-
"Expectation" 各プレーヤーの平均利得 "MarginalDistributions" 各プレーヤーの利得の分布 "MultivariateDistribution" 全プレーヤーの利得の多変量分布 "Simulation" ゲームの1ラウンドあたりの利得のランダムに生成されたリスト {"Simulation", n} 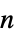 ラウンドのゲームについての利得のリスト
ラウンドのゲームについての利得のリスト"Variance" 各プレーヤーの利得の多変量分布
例題
すべて開くすべて閉じる例 (4)
スコープ (5)
アプリケーション (7)
社会ゲーム (2)
ボランティアのジレンマは,各プレーヤーがボランティアに参加することもしないこともできる状況を表している.少なくとも1人のプレーヤーがボランティアに参加すると他のすべてのプレーヤーがボランティアに参加しないことで少額の利益を得る.誰もボランティアの作業をしないと全員の利得が非常に低くなる.ボランティア作業をする人としない人がいるボランティアのジレンマゲームを生成する:
ボランティアに参加する可能性が高い人と可能性が低い人の期待利得を求める:
非協力ゲームは調整ゲームと非調整ゲームのハイブリッドで,プレーヤーの一人のインセンティブが協力することであるのに他のプレーヤーはそれを拒否しようとするものを言う.ボランティアの参加者と非参加者がいるボランティアのジレンマゲームを生成する:
経済ゲーム (2)
軍事ゲーム (1)
交通ゲーム (1)
驚くべきことに,道路網に1本あるいはそれ以上の道路を加えると交通が全体的に遅くなることがある.これはブライスのパラドックスとして知られているものである.a から b までの道路網がある場合,c または d を介して2つの異なる道路網を使用するとする.道路 ac と db は20 n 分かかる.ここで,n は道路上のドライバーの数である.cb と ad はドライバーの数には関係なく45分かかる.道路網をグラフとして表す:
ドライバーの数を n=2として,a から b へのすべての経路を求める:
通勤者が選択した異なる経路に対応する2つの純粋な戦略がある:
上記の交通ゲームを追いながら,モデリングを自動化し一般的な道路網を解く.ここで,start end は車の出発点と到達点であり,道路の各部分の容量は辺重みを使って符号化されている:
この状況は2人のドライバーのための新たな交通ゲームを定義する:
既存の2つの経路間で切り替えると,唯一の安定解では通勤時間は制限された道路網(65分)よりも長く(82分)なるという囚人のジレンマのような状態になる:
テキスト
Wolfram Research (2025), MatrixGamePayoff, Wolfram言語関数, https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
CMS
Wolfram Language. 2025. "MatrixGamePayoff." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MatrixGamePayoff.html.
APA
Wolfram Language. (2025). MatrixGamePayoff. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixGamePayoff.html