NestTree
NestTree[f,tree]
对 tree 的每个叶子添加孩子,f[expr] 给出数据为 expr 的叶子的新孩子的数据列表.
NestTree[f,tree,n]
对每个叶子的数据连续应用 f,直到第 n 层,为每个叶子最多增加 n 层.
NestTree[f,tree,n,h]
额外将 h 应用于新子树的数据.
NestTree[f,expr,…]
通过将 f 嵌套应用于数据为 expr 的叶子构建树.
更多信息和选项


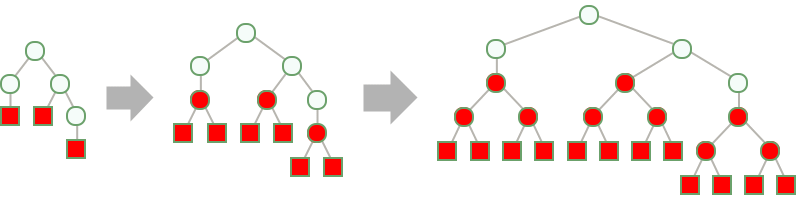
- NestTree 生成 Tree 对象,通过应用 f 对叶子连续添加更深层的孩子:
- NestTree 对于根据表达式构造树和扩展树的叶子很有用.
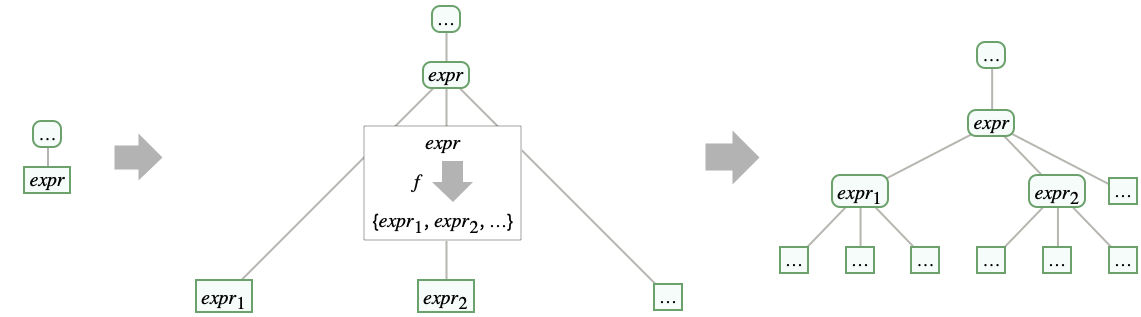
- 对于每一层新的嵌套,每个叶子 Tree[expr,None] 被 Tree[expr,{Tree[expr1,None],…}] 替换,其中 f[expr] 给出 {expr1,expr2,…}: »
- 在 NestTree[f,tree,n] 中,n 可以是任意非负机器整数或 Infinity. »
- NestTree[f,tree,n] 最多额外为每个叶子添加 n 层. 如果 f 返回 None、{}、<> 或 Hold[],则不会再为该叶子添加更多的层. »
- 在 NestTree[f,tree,n,h] 中,每个叶子 Tree[expr,None] 被 Tree[h[expr],…] 替换,包括原始叶子和那些在中间步骤生成的叶子. »
- 如果 expr 不是显式的 Tree 对象,则 NestTree[f,expr,…] 等价于 NestTree[f,Tree[expr,None],…]. »
- 如果 f[expr] 给出 Hold[expr1,expr2,…],则表达式 expri 被赋予函数 f,且不对 NestTree[f,tree,n,h] 中的 h 进行计算. »
- 在 NestTree[f,tree] 中,f[expr] 应给出 {expr1,expr2,…}、<key1expr1,key2expr2,…> Hold[expr1,expr2,…] 或 None.
- 如果 f 没有返回 {…}、<|…|>、Hold[…] 或 None,则 NestTree[f,tree,…] 等价于 NestTree[List@*f,tree,…]. »
- NestTree[f,tree,0] 给出 tree. NestTree[f,tree,0,h] 等价于 TreeMap[h,tree,{-1}].
- 如果 f[expr] 给出 <key1expr1,key2expr2,…>,则 NestTree[f,expr,n] 给出 Tree[expr,<key1tree1,key2tree2,…>],其中 treei 是 NestTree[f,expri,n-1] 的结果. »
- NestTree 与 Tree 的选项一样.
范例
打开所有单元关闭所有单元范围 (9)
选项 (9)
树图布局和图形选项 (3)
应用 (8)
定义一个可以将 TextElement 对象转换为树图的函数:
定义一个可以生成 TextElement 孩子元素的函数:
定义一个可以提取 TextElement 中的 "GrammaticalUnit" 的函数:
将 TextElement 转换为树图:
属性和关系 (12)
NestList 给出将运算符 f 连续应用于表达式的结果列表:
NestTree 给出将运算符 f 连续应用于表达式的结果的树:
NestTree 将后续运算符应用于列表的每个元素:
如果 expr 不是树,则 NestTree[f,expr,…] 根据表达式 expr 构建树:
这相当于 NestTree[f,Tree[expr,None],…]:
如果 f 没有返回 {…}、<|…|>、Hold[…] 或 None,则 NestTree[f,tree,…] 等价于 NestTree[List@*f,tree,…]:
NestTree[f,Tree[expr,None],0] 给出 Tree[expr,None]:
如果 f[expr] 给出 None,则 NestTree[f,Tree[expr,None]] 给出 Tree[expr,None]:
如果 f[expr] 给出 {…} 或 Hold[…],则 NestTree[f,Tree[expr,None]] 给出 Tree[expr,{…}]:
即便 f[expr] 给出 {} 或 Hold[],下式也成立:
NestTree 连续应用运算符 f,直到达到最大层级或 f 返回 None、{}、<> 或 Hold[]:
NestTree[f,Tree[expr,None],n,h] 给出数据为 h[expr] 的树和孩子 NestTree[f,Tree[expri,None],n-1,h],其中 f[expr] 给出 {expr1,expr2,…}:
NestTree[TreeChildren,Tree[tree,None],Infinity,TreeData] 等价于 tree:
NestGraph 将运算符应用于图中的每个顶点:
NestTree 将算符应用于树的每个叶子:
用 NestTree 模仿 CompleteKaryTree 的输出:
将树转换为实际的 Graph 对象:
生成含有从 0 到 10 的随机整数的树,对于内部子树生成 1 到 3 个孩子:
用 RandomTree 生成一定大小的随机树:
文本
Wolfram Research (2021),NestTree,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NestTree.html (更新于 2022 年).
CMS
Wolfram 语言. 2021. "NestTree." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/NestTree.html.
APA
Wolfram 语言. (2021). NestTree. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NestTree.html 年