ObservabilityGramian

ObservabilityGramian[ssm]

状態空間モデル ssm の可観測性グラミアンを与える．

詳細とオプション

  • 状態空間モデル ssm はStateSpaceModel[{a,b,c,d}]として与えられる．ただし，a，b，c，d は連続時間系あるいは離散時間系のどちらかにおける状態，入力，出力，伝送の各行列を表す．
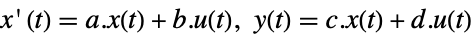
  • 連続時間系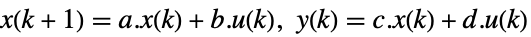
    離散時間系
  • 可観測性グラミアン
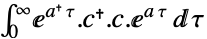
  • 連続時間系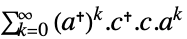
    離散時間系
  • 漸近的に安定した系では，グラミアン 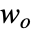はリャプノフ(Lyapunov)方程式の解として計算できる．
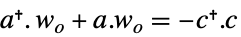
  • 連続時間系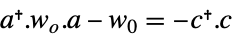
    離散時間系
  • ディスクリプタ行列があるStateSpaceModelについて，ObservabilityGramianは行列のペア{wos,wof}を返す．ただし，wos た遅い部分系に関連しており，wof は速い部分系に関連している．
  • 可観測性グラミアンはあるλについてDet[λ e-a]≠0であるディスクリプタ系についてのみ存在する．

例題

すべて開くすべて閉じる

例  (1)

ある系の可観測性グラミアン：

スコープ  (4)

連続時間系の可観測性グラミアン：

離散時間系の可観測性グラミアン：

記号系の可観測性グラミアン：

ディスクリプタ系の可観測性グラミアン：

アプリケーション  (1)

系が可観測であるかどうか確認する：

特性と関係  (7)

可観測性グラミアンは，双対系の可制御性グラミアンである：

可観測性グラミアンは状態行列の次元を持つ：

可観測性グラミアンがフルランクの場合，その系は可観測である：

可観測で漸近的に安定した系の可観測性グラミアンは対称かつ正定値である：

連続時間（離散時間）系の可観測性グラミアンは連続（離散）リャプノフ方程式を満足する：

ディスクリプタ系は2つの可観測性グラミアンを与える：

これらの系は，総和が正定値であるときかつそのときに限り，完全に可観測である：

速い部分系と遅い部分系のグラミアンは，クロネッカー分解から計算される：

分離された状態を分ける：

遅い部分系は，遅い状態のグラミアンと零行列を返す：

速い部分系は，速い状態のグラミアンと零行列を返す：

クロネッカー変換の逆変換はもとの系のグラミアンを与える：

これはObservabilityGramianを直接使った場合と同じ結果を与える：

考えられる問題  (1)

漸近的に安定ではない系については可観測性グラミアンは定義されない：

Wolfram Research (2010), ObservabilityGramian, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservabilityGramian.html （2012年に更新）.

テキスト

Wolfram Research (2010), ObservabilityGramian, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservabilityGramian.html （2012年に更新）.

CMS

Wolfram Language. 2010. "ObservabilityGramian." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/ObservabilityGramian.html.

APA

Wolfram Language. (2010). ObservabilityGramian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservabilityGramian.html

BibTeX

@misc{reference.wolfram_2024_observabilitygramian, author="Wolfram Research", title="{ObservabilityGramian}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ObservabilityGramian.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_observabilitygramian, organization={Wolfram Research}, title={ObservabilityGramian}, year={2012}, url={https://reference.wolfram.com/language/ref/ObservabilityGramian.html}, note=[Accessed: 18-November-2024 ]}