OutputControllabilityMatrix

OutputControllabilityMatrix[ssm]

状態空間モデル ssm の出力可制御性行列を与える．

詳細

  • 状態空間モデル ssm はStateSpaceModel[{a,b,c,d}]で与えられる．ただし，a，b，c，d は連続時間系あるいは離散時間系における状態，入力，出力，伝送の各行列を表す．
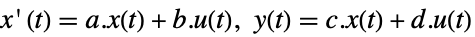
  • 連続時間系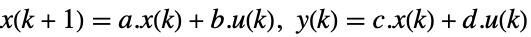
    離散時間系
  • 出力可制御性行列は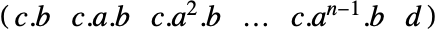で与えられる．ただし 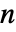は正方状態行列 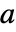の次元である．
  • ディスクリプタ状態空間モデルについては，OutputControllabilityMatrixは行列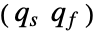を返す．ただし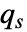，は遅い部分系に関連し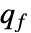，は速い部分系に関連している．
  • 特異ディスクリプタ行列 e を持つStateSpaceModel[{a,b,c,d,e}]では，出力可制御性行列は遅い部分系と速い部分系を分離することで計算される．
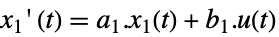
  • 遅い部分系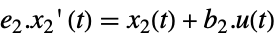
    速い部分系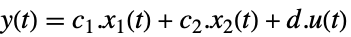
    出力方程式
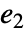  • がベキ零指標 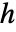を持つ出力可制御性行列は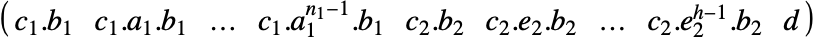で与えられる．
  • OutputControllabilityMatrixは，ある種の λ について Det[λ e - a]≠0であるディスクリプタ系のみを取る．

例題

すべて開くすべて閉じる

例  (1)

状態空間モデルの出力可制御性行列：

スコープ  (2)

連続時間系の出力可制御性行列：

ディスクリプタ系：

特性と関係  (4)

行列の階数が出力数と等しいとき，その系は出力可制御である：

この系は出力可制御ではないが状態可制御である：

この系は出力可制御ではあるが状態可制御ではない：

出力可制御性行列はサンプリング周期に依存しない：

Wolfram Research (2010), OutputControllabilityMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html （2012年に更新）.

テキスト

Wolfram Research (2010), OutputControllabilityMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html （2012年に更新）.

CMS

Wolfram Language. 2010. "OutputControllabilityMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html.

APA

Wolfram Language. (2010). OutputControllabilityMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html

BibTeX

@misc{reference.wolfram_2024_outputcontrollabilitymatrix, author="Wolfram Research", title="{OutputControllabilityMatrix}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_outputcontrollabilitymatrix, organization={Wolfram Research}, title={OutputControllabilityMatrix}, year={2012}, url={https://reference.wolfram.com/language/ref/OutputControllabilityMatrix.html}, note=[Accessed: 18-November-2024 ]}