PathGraphQ

PathGraphQ[g]

グラフ g が経路であればTrueを，その他の場合はFalseを返す．

詳細

  • 無向経路グラフは各頂点の次数が最高で2の連結グラフである．
  • 有向経路グラフは各頂点の入次数と出次数が最高で1の連結グラフである．

例題

すべて開くすべて閉じる

例  (2)

グラフが経路かどうか調べる：

頂点次数は最高でも2である：

完全グラフは経路ではない：

頂点次数が2よりも大きい：

スコープ  (6)

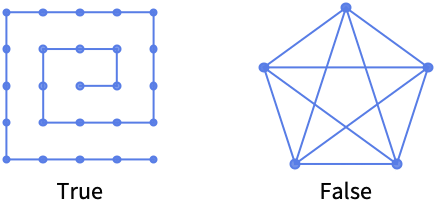
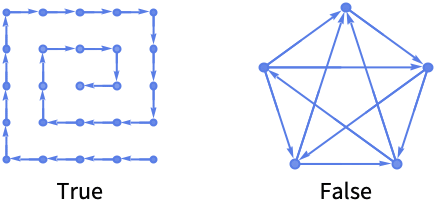
PathGraphQは無向グラフに使うことができる：

有向グラフに：

多重グラフに：

混合グラフに：

経路グラフではないものに対しては，PathGraphQはFalseを返す：

大きいグラフを調べる：

特性と関係  (8)

頂点の数が2以上の経路グラフにはループはない：

経路グラフには常に辺がある訳ではない：

始まりと終りが同一の頂点である経路グラフは巡回グラフである：

繰り返される頂点のない経路グラフは木グラフである：

非巡回経路グラフは単純グラフである：

二部グラフでもある：

GridGraph[{1,…,1,k,1,…,1}]はすべて経路グラフである：

経路グラフは連結グラフであり，各頂点の次数は最大で2である：

経路グラフ の線グラフは と同型である：

考えられる問題  (1)

明示的ではないグラフに対しては，PathGraphQはFalseを返す：

Wolfram Research (2010), PathGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/PathGraphQ.html.

テキスト

Wolfram Research (2010), PathGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/PathGraphQ.html.

CMS

Wolfram Language. 2010. "PathGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PathGraphQ.html.

APA

Wolfram Language. (2010). PathGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PathGraphQ.html

BibTeX

@misc{reference.wolfram_2024_pathgraphq, author="Wolfram Research", title="{PathGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PathGraphQ.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pathgraphq, organization={Wolfram Research}, title={PathGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/PathGraphQ.html}, note=[Accessed: 25-November-2024 ]}