PauliMatrix
PauliMatrix[k]
给出第 k![]() 个泡利自旋矩阵
个泡利自旋矩阵 ![]() .
.
更多信息和选项

- PauliMatrix 给出 2×2 常矩阵,它具有属性
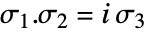 .
. - PauliMatrix[0] 和 PauliMatrix[4] 给出恒等矩阵.
- 可提供以下选项:
-
TargetStructure Automatic 返回矩阵的结构 WorkingPrecision Infinity 创建项的精度 - TargetStructure 的可能设置包括:
-
Automatic 自动选择返回的表示形式 "Dense" 以稠密矩阵的形式表示矩阵 "Hermitian" 以厄米特矩阵的形式表示矩阵 "Sparse" 以稀疏数组的形式表示矩阵 "Unitary" 以酉矩阵的形式表示矩阵 - 设置 TargetStructureAutomatic,则会返回稠密矩阵.
范例
打开所有单元关闭所有单元范围 (1)
PauliMatrix 按元素线性作用于列表:
选项 (6)
Wolfram Research (2008),PauliMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PauliMatrix.html (更新于 2024 年).
文本
Wolfram Research (2008),PauliMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PauliMatrix.html (更新于 2024 年).
CMS
Wolfram 语言. 2008. "PauliMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/PauliMatrix.html.
APA
Wolfram 语言. (2008). PauliMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PauliMatrix.html 年