Rationalize

Rationalize[x]

近似数 x を分母が小さい近傍の有理数に変換する．

Rationalize[x,dx]

x から dx 以内にある分母が最小の有理数を返す．

詳細

  • Rationalize[x,dx]は厳密な数 x に使うことができる．
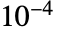  • をとしたときの条件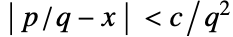を満足する x が十分近くにない場合，Rationalize[x]は x を変換せずにおく．
  • Rationalize[x,0]は，任意の非厳密数 x を有理形式に変換する． »

例題

すべて開くすべて閉じる

例  (1)

有理数に変換する：

スコープ  (5)

与えられた許容度の範囲内で有理近似を行う：

Rationalizeは厳密数に使うことができる：

式中のすべての数を有理化する：

デフォルトで，N[Pi]に十分近いとはみなされる有理数はない：

強制的に有理近似を行う：

アプリケーション  (3)

連続的な の有理近似：

次第によくなる の有理近似の誤差をプロットする：

次第によくなる近似の誤差をプロットする：

近似数係数で多項式を作る：

有理数しか含まないおおまかな近似を求める：

結果を因数分解する：

特性と関係  (3)

Rationalizeが有理数 を返す場合は，である：

Rationalize[x]が x を変化させずに返す場合は，これを満足する有理数は存在しない：

機械精度で最小分母誤差 dx の有理近似を得る：

不等式の剰余はこの有理近似すべてについて正である：

SetPrecision[x,∞]とRationalize[x,0]は，ともに実数 x の有理近似を返す：

Rationalize[x,0]は x の精度まで x に等しい有理数を返す：

SetPrecision[x,∞]は x のビットによる表現から直接有理数を得る：

RationalizeとRootApproximantは，どちらも実数 x を近似した厳密な数量を返す：

RootApproximant[x]は x の精度まで x と等しい代数的数を返す：

Rationalize[x,0]は x の精度まで x と等しい有理数を返す：

Wolfram Research (1988), Rationalize, Wolfram言語関数， https://reference.wolfram.com/language/ref/Rationalize.html （1999年に更新）.

テキスト

Wolfram Research (1988), Rationalize, Wolfram言語関数， https://reference.wolfram.com/language/ref/Rationalize.html （1999年に更新）.

CMS

Wolfram Language. 1988. "Rationalize." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1999. https://reference.wolfram.com/language/ref/Rationalize.html.

APA

Wolfram Language. (1988). Rationalize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rationalize.html

BibTeX

@misc{reference.wolfram_2024_rationalize, author="Wolfram Research", title="{Rationalize}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/Rationalize.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rationalize, organization={Wolfram Research}, title={Rationalize}, year={1999}, url={https://reference.wolfram.com/language/ref/Rationalize.html}, note=[Accessed: 22-December-2024 ]}