SiegelTheta

SiegelTheta[Ω,s]

シーゲル(Siegel)のシータ関数 を，リーマンモジュール行列 Ω とベクトル s とともに与える．

SiegelTheta[{ν1,ν2},Ω,s]

シーゲルのシータ関数 を指標 ν1，ν2とともに与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 行列 Ω は対称で，正の有限な虚部を持たなければならない．
  • Ω が p×p 行列の場合，ベクトル s と v あるいは νiは長さ p でなければならない．
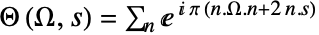  • ，ただし n は p 次の整数格子において可能なすべてのベクトルの範囲に及ぶものとする．
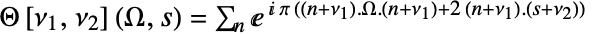  • ，ただし n の範囲は p 次元の整数格子上の可能なすべてのベクトルに及ぶものとする．
  • SiegelThetaは任意の数値精度で評価できる．

例題

すべて開くすべて閉じる

例  (3)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

スコープ  (7)

数値評価  (3)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

高精度で効率的に評価する：

特定の値  (2)

ゼロにおける値：

Re[SiegelTheta[{{I,1},{1, I}},{x,x/3}]]=1となるような x の値を求める：

可視化  (2)

SiegelTheta関数をさまざまなパラメータについてプロットする：

の実部をプロットする：

の虚部をプロットする：

一般化と拡張  (2)

指標 と を持つSiegelTheta：

特殊関数について記号的に簡約した指標を持つSiegelTheta：

アプリケーション  (2)

複素平面におけるSiegelThetaの絶対値をプロットする：

アーベル(Abel)の関数を定義する：

実部のプロット：

特性と関係  (2)

一次元では，SiegelThetaはEllipticTheta関数と一致する：

SiegelThetaこれらの方程式を満足する：

考えられる問題  (2)

SiegelThetaは対称な 行列を必要とする：

対称な部分：

機械精度では正しい答を求めるには不十分なことがある：

任意精度を使って結果を検証する：

おもしろい例題  (1)

ネストしたSiegelTheta関数における正値性からの偏差を可視化する：

Wolfram Research (2007), SiegelTheta, Wolfram言語関数， https://reference.wolfram.com/language/ref/SiegelTheta.html.

テキスト

Wolfram Research (2007), SiegelTheta, Wolfram言語関数， https://reference.wolfram.com/language/ref/SiegelTheta.html.

CMS

Wolfram Language. 2007. "SiegelTheta." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SiegelTheta.html.

APA

Wolfram Language. (2007). SiegelTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SiegelTheta.html

BibTeX

@misc{reference.wolfram_2024_siegeltheta, author="Wolfram Research", title="{SiegelTheta}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/SiegelTheta.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_siegeltheta, organization={Wolfram Research}, title={SiegelTheta}, year={2007}, url={https://reference.wolfram.com/language/ref/SiegelTheta.html}, note=[Accessed: 22-November-2024 ]}