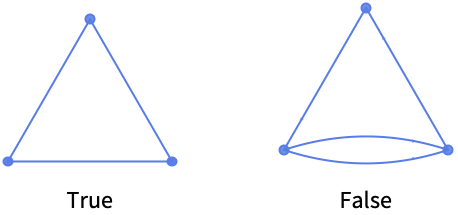
SimpleGraphQ

SimpleGraphQ[g]

グラフ g が単純グラフの場合にはTrueを，それ以外の場合にFalseを返す．

詳細

  • あるグラフに同一頂点間の自己ループや多重辺がない場合，そのグラフは単純グラフである．

例題

すべて開くすべて閉じる

例  (2)

グラフが単純グラフかどうか調べる：

すべてのグラフが単純グラフである訳ではない：

スコープ  (5)

SimpleGraphQは無向グラフに使うことができる：

有向グラフに：

多重グラフに：

混合グラフに：

SimpleGraphQは大きいグラフに使うことができる：

特性と関係  (8)

自己ループのあるグラフは単純グラフではない：

単純グラフは巡回グラフであることもある：

単純グラフが二部グラフであることもある：

PathGraphは常に単純グラフである：

単純グラフの隣接行列の対角項は0である：

単純グラフの結合行列には-1，0あるいは1の項がある：

単純グラフの頂点の最大次数はどれも頂点数より低い：

自明ではない単純グラフには次数が等しい頂点ペアが少なくとも1つなければならない：

考えられる問題  (2)

単純グラフには同じ頂点間に方向が異なる2辺があってもよい：

明示的ではないグラフに対してはSimpleGraphQはFalseを与える：

Wolfram Research (2010), SimpleGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/SimpleGraphQ.html.

テキスト

Wolfram Research (2010), SimpleGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/SimpleGraphQ.html.

CMS

Wolfram Language. 2010. "SimpleGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SimpleGraphQ.html.

APA

Wolfram Language. (2010). SimpleGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SimpleGraphQ.html

BibTeX

@misc{reference.wolfram_2024_simplegraphq, author="Wolfram Research", title="{SimpleGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SimpleGraphQ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_simplegraphq, organization={Wolfram Research}, title={SimpleGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/SimpleGraphQ.html}, note=[Accessed: 22-November-2024 ]}