SingularValues[m]
gives the singular value decomposition for a numerical matrix ![]() . The result is a list
. The result is a list ![]() , where
, where ![]() is the list of singular values, and
is the list of singular values, and ![]() can be written as ConjugateTranspose[u]. DiagonalMatrix[w].v.
can be written as ConjugateTranspose[u]. DiagonalMatrix[w].v.


SingularValues
SingularValues[m]
gives the singular value decomposition for a numerical matrix ![]() . The result is a list
. The result is a list ![]() , where
, where ![]() is the list of singular values, and
is the list of singular values, and ![]() can be written as ConjugateTranspose[u]. DiagonalMatrix[w].v.
can be written as ConjugateTranspose[u]. DiagonalMatrix[w].v.
Details and Options
- SingularValues[m,Tolerance->t] specifies that singular values smaller than t times the maximum singular value are to be removed.
- The default setting Tolerance->Automatic typically takes
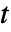 to be
to be 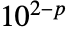 where
where 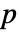 is the numerical precision of the input.
is the numerical precision of the input. - With Tolerance->0 singular values which are exactly zero can be returned.
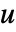 and
and 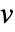 are row orthonormal matrices, which can be considered as lists of orthonormal vectors.
are row orthonormal matrices, which can be considered as lists of orthonormal vectors.- The ratio of the largest to smallest singular value gives the
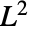 condition number of
condition number of 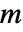 .
.
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), SingularValues, Wolfram Language function, https://reference.wolfram.com/language/ref/SingularValues.html.
CMS
Wolfram Language. 1988. "SingularValues." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SingularValues.html.
APA
Wolfram Language. (1988). SingularValues. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SingularValues.html
BibTeX
@misc{reference.wolfram_2025_singularvalues, author="Wolfram Research", title="{SingularValues}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/SingularValues.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_singularvalues, organization={Wolfram Research}, title={SingularValues}, year={1988}, url={https://reference.wolfram.com/language/ref/SingularValues.html}, note=[Accessed: 28-February-2026]}