StratonovichProcess

StratonovichProcess[{a,b},x,t]

Stratonovich過程 を表す．ただし，である．

StratonovichProcess[{a,b,c},x,t]

Stratonovich過程 を表す．ただし，である．

StratonovichProcess[…,…,{x,x0},{t,t0}]

初期条件 のStratonovich過程を表す．

StratonovichProcess[…,…,…,Σ]

共分散Σのウィナー(Wiener)過程 を使う．

StratonovichProcess[proc]

可能な際は常に proc を標準Stratonovich過程に変換する．

StratonovichProcess[sdeqns,expr,x,t,wdproc]

確率微分方程式 sdeqns，出力式expr，状態 x，時間 t で指定され，過程 dproc に従う w によって決定されるStratonovich過程を表す．

詳細とオプション

  • StratonovichProcessはStratonovich拡散あるいは確率微分方程式としても知られている．
  • StratonovichProcessは連続時間・連続状態のランダム過程である．
  • ドリフト a が 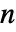次元ベクトルで拡散 b が 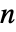× 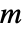次元の行列の場合，この過程は 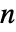次元であり 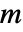次元のWienerProcessによって決定される．
  • 係数 a および b の一般的な指定値
  • a スカラー, b スカラー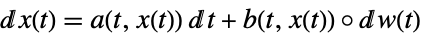
    a スカラー, b ベクトル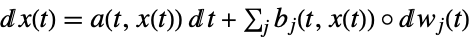
    a ベクトル, b ベクトル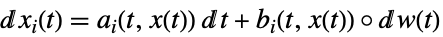
    a ベクトル, b 行列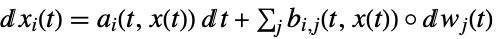
  • 確率微分方程式 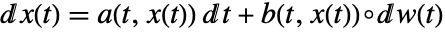は積分方程式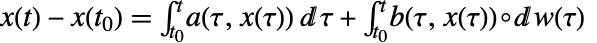として書かれることもある．
  • デフォルトの初期時間 t0 は0であるとみなされる．デフォルトの初期状態 x0 は0である．
  • デフォルトの共分散Σは恒等行列である．
  • 標準Stratonovich過程の出力は微分状態 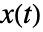のサブセットからな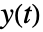る である．
  • 標準StratonovichProcess形式に変換可能な過程 proc は，OrnsteinUhlenbeckProcess，GeometricBrownianMotionProcess，ItoProcess，StratonovichProcess等である．
  • sdeqns における確率微分方程式は 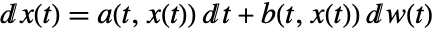の形でよい．ただし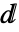， は\[DifferentialD]で，これはddとして入力する．微分 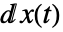および 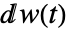はStratonovich微分であると解釈される．
  • 出力式 expr は x[t] および t を含む任意の式でよい．
  • 駆動過程 dproc は標準Stratonovich過程に変換可能な任意の過程でよい．
  • 次は，StratonovichProcessの関連特性である．
  • "Drift"ドリフト項
    "Diffusion"拡散行列
    "Output"出力状態
    "TimeVariable"時間変数
    "TimeOrigin"時間変数の原点
    "StateVariables"状態変数
    "InitialState"初期状態値
    "KolmogorovForwardEquation"Kolmogorov前進方程式（Fokker-Planckの方程式）
    "KolmogorovBackwardEquation"Kolmogorov後退方程式
    "Derivative"Stratonovich導関数
  • StratonovichProcessに特有のRandomFunctionにおけるMethod設定 »
  • "EulerMaruyama"オイラー・丸山（次数1/2，デフォルト）
    "KloedenPlatenSchurz"Kloeden-Platen‐Schurz（次数3/2）
    "Milstein"Milstein（次数1）
    "StochasticRungeKutta"3段階Rossler SRKスキーム（次数1）
    "StochasticRungeKuttaScalarNoise"スカラーノイズのための3段階Rossler SRKスキーム（次数3/2）
  • StratonovichProcessは，RandomFunction，CovarianceFunction，PDF，Expectation等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (1)

過程をその確率微分方程式で定義する：

過程のシミュレーションを行う：

平均値関数を計算する：

共分散関数を計算する：

スコープ  (16)

基本的な用法  (10)

ドリフト ，拡散 のウィナー過程を確率微分方程式 から定義する：

パラメトリック過程から直接変換する：

過程 を定義する，ただし である：

微分記法を使って同じ過程を定義する：

出力 のベクトル過程 を定義する：

微分記法を使って：

ベクトル過程 を定義する．ただし である：

微分記法を使って：

ベクトル過程 を定義する．ただし である：

微分記法を使って：

2つの相関ウィナー過程によって牽引される過程を定義する：

確率微分方程式 に対応するスカラー過程 を定義する：

確率微分方程式 および に対応するベクトル過程 および を定義する：

2D相関ウィナー過程に対応する過程を定義する：

2D相関ウィナー過程に牽引されるベクトル過程を定義する：

さまざまなメソッドを使ってStratonovichProcessの経路のシミュレーションを行う：

シミュレーションメソッドと対応する次数：

シミュレーションメソッドをRandomFunctionのオプションとして指定する：c

過程特性の抽出  (1)

確率微分方程式でStratonovich過程を定義する：

使用可能なStratonovich過程の特性：

過程のドリフトと拡散：

Kolmogorov前進方程式：

ここではInactiveを使って偏導関数を展開しないようにしている．式の展開にはActivateを使う：

Kolmogorov後退方程式：

関数 のStratonovich導関数を計算する．出力はドリフト項と拡散項からなるリストである：

特殊Stratonovich過程  (5)

WienerProcessに対応するStratonovich過程：

GeometricBrownianMotionProcessに対応するStratonovich過程：

BrownianBridgeProcessに対応するStratonovich過程：

OrnsteinUhlenbeckProcessに対応するStratonovich過程：

CoxIngersollRossProcessに対応するStratonovich過程：

アプリケーション  (3)

反復Stratonovich積分 , , , , , に対応するベクトル過程を定義する：

その平均値関数を計算する：

共分散関数も計算する：

熱変動の影響下での自由粒子のダイナミクスは，Langevin運動方程式 によってモデル化できる．ここで は標準のWienerProcessであり， は熱ノイズの強度である．ここでは， は にのみ依存し，速度の方程式に焦点を当てることができると想定されている．運動方程式の統合には，伊藤定式化とStratonovich定式化という一般的な2つの方法があるが，それらは次の方法で定義できる：

が定数のとき，2つの定式化は同一で，のときに同じ定常分布に至る：

が速度に依存する場合は，WienerProcessの性質のために，は非零の二次変動を持ち，2つの定式化は異なる結果をもたらす．伊藤の公式をStratonovichの公式相当に変換する：

Stratonovichの定式化でのドリフトは伊藤の定式化でのドリフトとは異なる：

OrnsteinUhlenbeckProcessを作成し，StratonovichProcessでこれを表す：

Kolmogorov前進方程式を得る：

，における局所化された初期条件，ディリクレ境界条件で方程式を数値的に解く：

Kolmogorov前進方程式の における解をプロットし，これを閉じた形の密度関数と比較する：

Animateで解のダイナミクスを可視化する：

特性と関係  (1)

ItoProcessをStratonovichProcessに変換する：

変換し戻す：

考えられる問題  (2)

StratonovichProcessはランダムな初期条件をサポートしないので，表すことができない：

しかし，固定した初期条件の過程はサポートする：

駆動された過程の初期時間はStratonovichProcessとマッチする必要が有る：

初期時間がマッチすると表すことができる：

Wolfram Research (2012), StratonovichProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StratonovichProcess.html.

テキスト

Wolfram Research (2012), StratonovichProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StratonovichProcess.html.

CMS

Wolfram Language. 2012. "StratonovichProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StratonovichProcess.html.

APA

Wolfram Language. (2012). StratonovichProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StratonovichProcess.html

BibTeX

@misc{reference.wolfram_2024_stratonovichprocess, author="Wolfram Research", title="{StratonovichProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StratonovichProcess.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_stratonovichprocess, organization={Wolfram Research}, title={StratonovichProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/StratonovichProcess.html}, note=[Accessed: 22-November-2024 ]}