TreeGamePayoff
TreeGamePayoff[tgame,strat]
gives the expected payoff for each player in the tree game tgame with strategy profile strat.
TreeGamePayoff[tgame,strat,adv]
gives the expected payoff for each player in the tree game tgame with the incomplete strategy profile strat and the adversary type adv.
Details

- TreeGamePayoff is also known as the expected payoff or the expected utility of a sequential game.
- TreeGamePayoff is typically used to evaluate expected payoffs for players given strategies for each of the players.
- A tree game strategy <…,playeri<{ni,1}pri,1,…,{ni,mi}pri,mi>,…> specifies the action probabilities pri,j for playeri in action node ni,j for playeri.
- The expected payoff pi for player i at the action node nj with mj choices is given by pi[{nj}]=
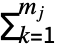 pi[{nj,k}].prj,k, while the expected payoff pi for player i at the end node nt is given by its specified payoff: pi[{nt}]=pi,j.
pi[{nj,k}].prj,k, while the expected payoff pi for player i at the end node nt is given by its specified payoff: pi[{nt}]=pi,j. - An incomplete tree strategy is a tree game strategy where only a subset of the action nodes have specified probabilities.
- For an incomplete strategy, the following specifications can be given for unspecified actions adv:
-
"Perfect" the payoffs of a random trial assuming an optimal choice for unspecified actions "PerfectExpectation" the average payoffs assuming an optimal random choice for unspecified actions "Random" the payoffs of a random trial assuming a uniform random choice for unspecified actions "RandomExpectation" the average payoffs assuming a uniform random choice for unspecified actions
Examples
open allclose allBasic Examples (3)
Scope (3)
Applications (5)
Social Games (3)
The Centipede game has two players who alternate in making decisions. At each turn, a player can choose between going "down" and ending the game or going "across" and continuing it (except at the last node where going "across" also ends the game). The longer the game goes on, the higher the total utility. A player who ends the game early will get a larger share of what utility there is. Consider a centipede game of three actions per player:
While the game-theoretic best solution is the pessimistic first choice, note that random players have a similar expected payoff. Compare the expected output of random and perfect players:
The tree game of Matching Pennies is a game where each of two people chooses either Head or Tail. If the choices differ, person 1 pays person 2 a dollar; if they are the same, person 2 pays person 1 a dollar. Generate a tree game of Matching Pennies:
Clearly, this game gives an advantage to player 2, making it impossible to get a better payoff against a perfect player. Imagine being player 1. Try several strategies to attempt to beat a perfect player (to have a payoff of 1):
An entry game is a game where an entrant decides whether to enter a market or not, and the incumbent decides whether to fight or accommodate the entrant if he enters. Generate an entry game:
Suppose that you are the incumbent player, and your strategy is to always fight (first choice). Find the expected payoff against a random player:
Perfect players assume perfect subgame equilibrium. Since that strategy is suboptimal, it turns out that the perfect player may have a worse payoff than the random player. Find the expected payoff against a perfect player:
Recreational Games (2)
Rock Paper Scissors is a zero-sum game, where either one player wins and the other loses, or there is a tie. Generate the tree version of this game, where the second player can choose an action considering the action of the first player:
Clearly, in the case of the tree game of Rock Paper Scissors, the second player can always choose the best action, and thus the first player is at a disadvantage by playing first. Write the perfect strategy in this version of Rock Paper Scissors:
Consider the game of tic-tac-toe. Design a function to generate the partial tic-tac-toe game between players A and B:
Consider a partially completed game of tic-tac-toe:
Form a TreeGame based on it:
If both players play perfectly, Player B wins:
If both players play randomly, player 2 is more likely to win only by a small margin:
Text
Wolfram Research (2025), TreeGamePayoff, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
CMS
Wolfram Language. 2025. "TreeGamePayoff." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
APA
Wolfram Language. (2025). TreeGamePayoff. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeGamePayoff.html