TreeGamePayoff
TreeGamePayoff[tgame,strat]
给出在具有策略概况 strat 的树状博弈 tgame 中每个玩家的预期收益.
TreeGamePayoff[tgame,strat,adv]
给出具有不完整策略概况 strat 和对手类型 adv 的树状博弈 tgame 中每个玩家的预期收益.
更多信息

- TreeGamePayoff 也被称为序贯博弈的预期收益或预期效用.
- TreeGamePayoff 通常用于评估给定每个参与者的策略的预期收益.
- 树状博弈策略 <…,playeri<{ni,1}pri,1,…,{ni,mi}pri,mi>,…> 指定 playeri 的动作节点 ni,j 中 playeri 的动作概率 pri,j.
- 当有 mj 个选择时,玩家 i 在动作节点 nj 的预期收益 pi 为 pi[{nj}]=
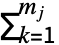 pi[{nj,k}].prj,k,而玩家 i 在终端节点 nt 的预期收益 pi 由其指定收益给出:pi[{nt}]=pi,j.
pi[{nj,k}].prj,k,而玩家 i 在终端节点 nt 的预期收益 pi 由其指定收益给出:pi[{nt}]=pi,j. - 不完全树策略是一种树形游戏策略,其中只有一部分动作节点具有指定的概率.
- 对于不完全策略,可以对未指定的动作 adv 给出以下规范:
-
"Perfect" 随机试验的收益,假定对未指定的行为做出最优选择 "PerfectExpectation" 平均收益,假定对未指定的行为做出最优随机选择 "Random" 随机试验的收益,假定对未指定的行为做出均匀随机选择 "RandomExpectation" 平均收益,假定对未指定的行为做出均匀随机选择
范例
打开所有单元关闭所有单元基本范例 (3)
应用 (5)
社会学博弈 (3)
蜈蚣游戏(Centipede game)有两名玩家轮流做决定. 在每个回合,玩家可以选择“向下”结束游戏,也可以选择“向右”继续游戏(除了最后一个节点,在最后一个节点“向右”也会结束游戏). 游戏时间越长,总收益越高. 提前结束游戏的玩家将获得更大的收益份额. 考虑一个每个玩家有三个动作的蜈蚣游戏:
虽然博弈论最佳解决方案是悲观的第一选择,但请注意,随机玩家的预期收益相似. 比较随机玩家和完美玩家的预期输出:
配对硬币(Matching Pennies)树游戏是两个人各自选择正面或反面的游戏. 如果选择不同,则第 1 个人向第 2 个人支付 1 美元;如果选择相同,则第 2 个人向第 1 个人支付 1 美元. 生成配对硬币树游戏:
显然,这个游戏给玩家 2 提供了优势,使得玩家 2 在与完美玩家的对战中不可能获得更好的收益. 想象一下成为玩家 1. 尝试几种策略来击败完美玩家(获得收益 1):
入场博弈是指进入者决定是否进入市场,而现有市场参与者则决定在新进入者进入后进行竞争还是接纳新进入者. 生成入场博弈:
休闲游戏 (2)
石头剪刀布是一个零和游戏,要么一个玩家赢,另一个玩家输,要么平局. 生成此游戏的树版本,其中第二个玩家可以根据第一个玩家的动作选择一个动作:
显然,在石头剪刀布的树状游戏中,第二个玩家总是可以选择最佳动作,因此第一个玩家先出手会处于劣势. 在此版本的石头剪刀布游戏中写下完美的策略:
以井字棋游戏为例. 设计一个函数来生成玩家 A 和 B 之间的部分井字棋游戏:
基于此形成一个 TreeGame:
文本
Wolfram Research (2025),TreeGamePayoff,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
CMS
Wolfram 语言. 2025. "TreeGamePayoff." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TreeGamePayoff.html.
APA
Wolfram 语言. (2025). TreeGamePayoff. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TreeGamePayoff.html 年