WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

WeaklyConnectedGraphQ
✖
WeaklyConnectedGraphQ

✖

グラフ g が弱連結の場合はTrueを，それ以外の場合はFalseを返す．

詳細

  • WeaklyConnectedGraphQは任意のグラフオブジェクトに使うことができる．
  • グラフは，すべての頂点ペアを繋ぐ連続する辺がある場合，弱連結グラフである．
  • グラフが無向であるとみなされるときに，すべての頂点ペアを連結する一連の辺がある場合，このグラフは弱連結である．

例題

すべて開くすべて閉じる

例  (2)基本的な使用例

グラフが弱連結かどうかを調べる：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-z3ym2a
Out[1]=1

孤立頂点があるグラフは弱連結グラフではない：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-4u1u68
Out[1]=1

スコープ  (6)標準的な使用例のスコープの概要

無向グラフを調べる：

In[2]:=2
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-8zzfce
Out[2]=2

有向グラフを調べる：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-xkbvj
Out[1]=1

多重グラフ：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-yyp8c5
Out[1]=1

混合グラフ：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-xb9nxo
Out[1]=1

WeaklyConnectedGraphQは，弱連結ではない任意のグラフについてFalseを与える：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-3l2bwe
Out[1]=1

WeaklyConnectedGraphQは，大きいグラフに使うことができる：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-pq9ae
In[2]:=2
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-cevvx1
Out[2]=2

特性と関係  (3)この関数の特性および他の関数との関係

ツリーグラフは弱連結である：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-edtvky
Out[1]=1
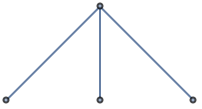
In[2]:=2
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-f2y3hj
Out[2]=2

経路グラフは弱連結である：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-chaumv
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-t11qf
Out[2]=2

個の頂点がある弱連結グラフ中の辺の最少数は である：

In[1]:=1
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-bge9sr
Out[1]=1
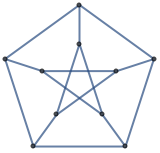
In[2]:=2
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-bdmabn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-igkijm
Out[3]=3

個の頂点がある経路グラフには，厳密に 本の辺がある：

In[4]:=4
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-iqoccl
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-hycp5h
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0g38x65i9p0wa7dxf-csa43m
Out[6]=6
Wolfram Research (2012), WeaklyConnectedGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.
✖
Wolfram Research (2012), WeaklyConnectedGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.

テキスト

Wolfram Research (2012), WeaklyConnectedGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.

✖
Wolfram Research (2012), WeaklyConnectedGraphQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.

CMS

Wolfram Language. 2012. "WeaklyConnectedGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.

✖
Wolfram Language. 2012. "WeaklyConnectedGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html.

APA

Wolfram Language. (2012). WeaklyConnectedGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html

✖
Wolfram Language. (2012). WeaklyConnectedGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html

BibTeX

@misc{reference.wolfram_2025_weaklyconnectedgraphq, author="Wolfram Research", title="{WeaklyConnectedGraphQ}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html}", note=[Accessed: 15-May-2025 ]}

✖
@misc{reference.wolfram_2025_weaklyconnectedgraphq, author="Wolfram Research", title="{WeaklyConnectedGraphQ}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html}", note=[Accessed: 15-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_weaklyconnectedgraphq, organization={Wolfram Research}, title={WeaklyConnectedGraphQ}, year={2012}, url={https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html}, note=[Accessed: 15-May-2025 ]}

✖
@online{reference.wolfram_2025_weaklyconnectedgraphq, organization={Wolfram Research}, title={WeaklyConnectedGraphQ}, year={2012}, url={https://reference.wolfram.com/language/ref/WeaklyConnectedGraphQ.html}, note=[Accessed: 15-May-2025 ]}