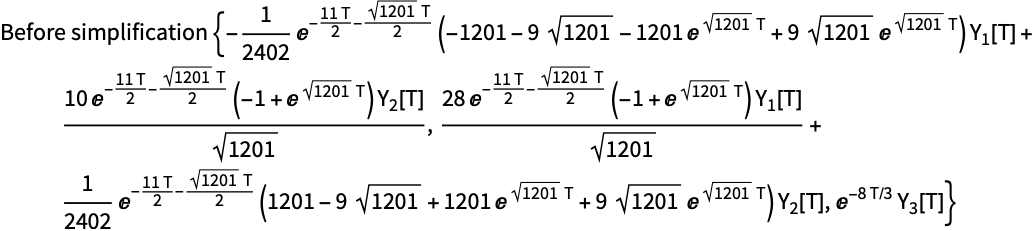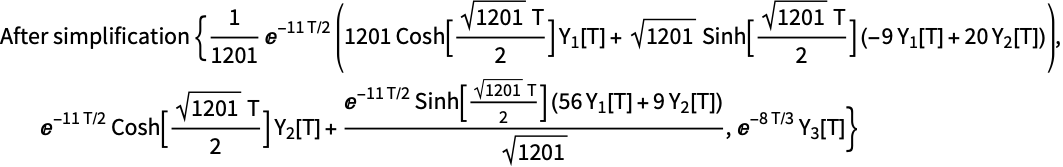NDSolveの"LocallyExact"メソッド
はじめに
微分方程式系は，解析法で解ける場合がある．このような既知のアルゴリズム技法の多くを，関数DSolveが実装する．
しかし，閉形式で解くことのできる微分方程式系は小さい部分集合しか構成しない．この事実に関わらず，ベクトル場全体で閉形式の解が存在しない場合，微分方程式系をベクトル場の部分について解析的に解くことができる場合がよくある．この例として"Splitting"メソッドがある．これはべクトル場 
を，
となるような 
という部分体に分割するものである．
"LocallyExact"メソッドとは基本的に，DSolveが解を見付けることができる場合，局所的に解を求めるために，標準的な数値積分スキームではなく数値評価を直接使うことができるというものである．
"LocallyExact"メソッドは刻み幅を適宜調整しようとはしないので，主として積分ステップ間のサブメソッドとして使われる．
例題
調和振動
大域と局所
"LocallyExact"メソッドは，閉形式の（大域的な）解に代るものではない．
"LocallyExact"メソッドは解を求めるために解析法を使うが，数値積分の格子点で（もしくは，正確には格子点の内側で）しか解を生成しない．従って，数値積分点上に正確には存在しない補間点での標本抽出のために，エラーが存在する可能性がある．
簡略化
"LocallyExact"メソッドには，DSolveの結果を簡略化するために使うことのできるオプション"SimplificationFunction"がある．
この部分系はDSolveで正確に解くことができる．
DSolveの結果は簡略化できることが多い．以下は式を簡略化する関数を定義し，入力と結果を出力する：
簡略化は，数値積分法のためのデータオブジェクトを構築する初期化段階で1度しか実行されない．