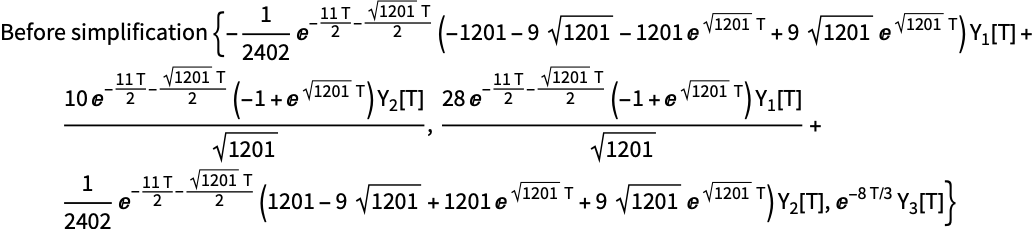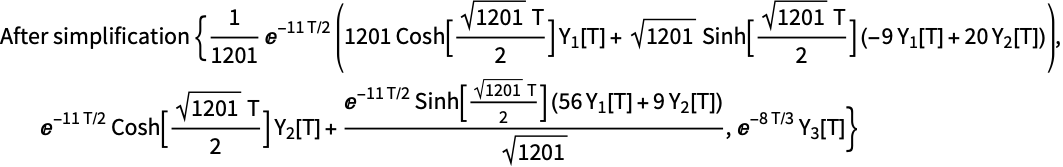NDSolve 的“LocallyExact”方法

引言选项总结
示例

引言

微分系统有时候可以采用解析的方法求解. 函数 DSolve 实现了许多已知的算法技术.

但是，可以采用闭合式求解的微分系统只占很小的一部分. 尽管如此，当一个解析解对于整个向量场不存在时，往往可能用解析方法对该向量场的一部分求解微分方程组. 这方面的一个例子是方法 "Splitting"，它把一个向量场 分解为一些子场 使得 .    

方法 "LocallyExact" 背后的思想是不使用一个标准数值积分方案，而是当一个解可以使用 DSolve 找到时，应用直接数值计算来局部推进解.

由于方法 "LocallyExact" 没有试图自适应调整步长，它主要是作为积分步之间的子方法使用.

示例

加载具有一些预定义问题的一个程序包：

谐振子

使用方法 "LocallyExact" 数值求解一个谐振子的运动方程. 结果是两个近似于解和第一导数的内插函数：
该解在单位圆上演化：

全局和局部的比较

方法 "LocallyExact" 的目的不是作为一个闭式（全局）解的替代品.

尽管事实是方法 "LocallyExact" 使用解析解来推动解，它只能产生数值积分中格点处的解（或者，恰当地说，是在格点内部）. 因此，由于在不精确处于数值积分网格的插值点上采样，有可能存在误差.

绘制谐振子解的第一个部分的误差，并且将它与精确流相比较：

简化

方法 "LocallyExact" 具有一个选项 "SimplificationFunction"，它可用于简化 DSolve 的结果.

下面是一个微分系统的线性部分，该系统出现在使用参数的标准值的 Lorenz 方程的分裂中：
该子系统使用 DSolve 精确可解：
通常 DSolve 的结果可以被简化. 这里定义一个函数来简化一个表达式，并且也打印出输入和结果：
该函数可以作为一个选项传递给方法 "LocallyExact"：

该简化过程只在构造数值积分方法的数据对象的初始化阶段执行一次.

选项总结

选项名
默认值
"SimplificationFunction"None用于简化 DSolve 结果的函数

方法 "LocallyExact" 的选项.